Problem
A square matrix is said to be an X-Matrix if both of the following conditions hold:
All the elements in the diagonals of the matrix are non-zero.
All other elements are 0.
Given a 2D integer array grid of size n x n representing a square matrix, return true** if grid is an X-Matrix**. Otherwise, return false.
Example 1:
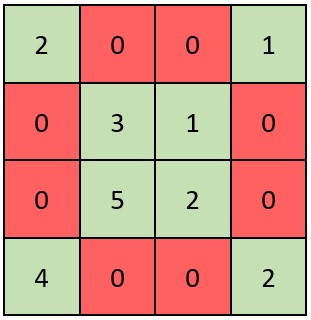
Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
Output: true
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
Example 2:
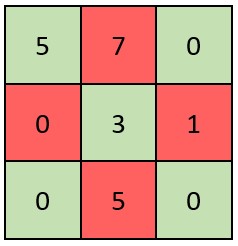
Input: grid = [[5,7,0],[0,3,1],[0,5,0]]
Output: false
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1000 <= grid[i][j] <= 10^5
Solution (Java)
class Solution {
public boolean checkXMatrix(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (i == j || i + j == grid.length - 1) {
if (grid[i][j] == 0) {
return false;
}
} else {
if (grid[i][j] != 0) {
return false;
}
}
}
}
return true;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).