894. All Possible Full Binary Trees

Problem

Given an integer n, return **a list of all possible *full binary trees* with** n nodes. Each node of each tree in the answer must have Node.val == 0.

Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

  Example 1:

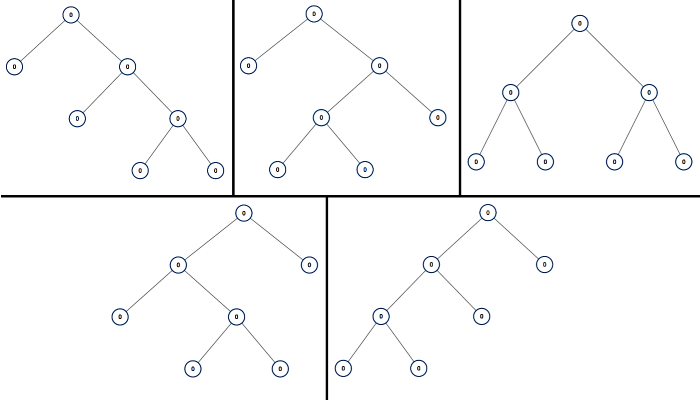
Input: n = 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

Example 2:

Input: n = 3
Output: [[0,0,0]]

  Constraints:

• 1 <= n <= 20

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<TreeNode> allPossibleFBT(int n) {
        if (n % 2 == 0) {
            // no complete binary tree possible
            return new ArrayList<>();
        }
        List<TreeNode>[] dp = new ArrayList[n + 1];
        // form left to right
        for (int i = 1; i <= n; i += 2) {
            helper(i, dp);
        }
        return dp[n];
    }

    // Using tabulation
    public void helper(int n, List<TreeNode>[] dp) {
        if (n <= 0) {
            return;
        }
        if (n == 1) {
            dp[1] = new ArrayList<>();
            dp[1].add(new TreeNode(0));
            return;
        }
        dp[n] = new ArrayList<>();
        for (int i = 1; i < n; i += 2) {
            // left
            for (TreeNode nodeL : dp[i]) {
                // right
                for (TreeNode nodeR : dp[n - i - 1]) {
                    // 1 node used here
                    TreeNode root = new TreeNode(0);
                    root.left = nodeL;
                    root.right = nodeR;
                    dp[n].add(root);
                }
            }
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).