Problem
You are given two non-empty linked lists representing two non-negative integers. The most significant digit comes first and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
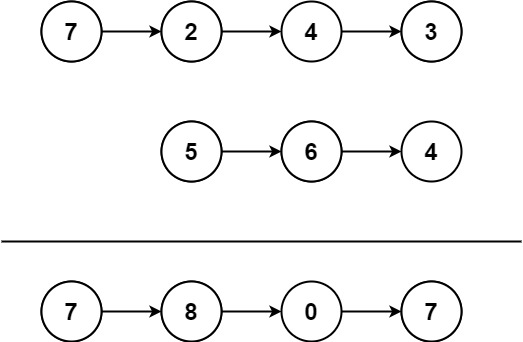
Input: l1 = [7,2,4,3], l2 = [5,6,4]
Output: [7,8,0,7]
Example 2:
Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [8,0,7]
Example 3:
Input: l1 = [0], l2 = [0]
Output: [0]
Constraints:
The number of nodes in each linked list is in the range
[1, 100].0 <= Node.val <= 9It is guaranteed that the list represents a number that does not have leading zeros.
Follow up: Could you solve it without reversing the input lists?
Solution (Java)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
private ListNode reverse(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode prev = null;
ListNode curr = head;
ListNode next = head.next;
while (next != null) {
curr.next = prev;
prev = curr;
curr = next;
next = next.next;
}
curr.next = prev;
return curr;
}
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
l1 = reverse(l1);
l2 = reverse(l2);
ListNode res = new ListNode();
ListNode head = res;
int carry = 0;
while (l1 != null || l2 != null) {
int val1;
int val2;
if (l1 == null) {
val1 = 0;
} else {
val1 = l1.val;
l1 = l1.next;
}
if (l2 == null) {
val2 = 0;
} else {
val2 = l2.val;
l2 = l2.next;
}
int data = val1 + val2 + carry;
if (data > 9) {
carry = data / 10;
data = data % 10;
} else {
carry = 0;
}
res.next = new ListNode(data);
res = res.next;
}
if (carry != 0) {
res.next = new ListNode(carry);
}
return reverse(head.next);
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).