Widest Vertical Area Between Two Points Containing No Points

Problem

Given n points on a 2D plane where points[i] = [xi, yi], Return** the *widest vertical area* between two points such that no points are inside the area.**

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

Example 1:

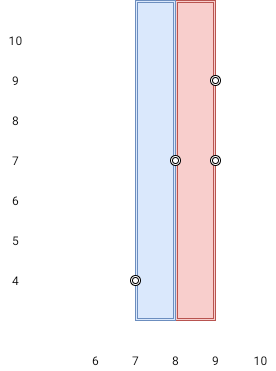
Input: points = [[8,7],[9,9],[7,4],[9,7]]
Output: 1
Explanation: Both the red and the blue area are optimal.

Example 2:

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
Output: 3

Constraints:

n == points.length
2 <= n <= 10^5
points[i].length == 2
0 <= xi, yi <= 10^9

Solution (Java)

class Solution {
    public int maxWidthOfVerticalArea(int[][] points) {
        int[] xValues = new int[points.length];
        for (int i = 0; i < points.length; i++) {
            xValues[i] = points[i][0];
        }
        Arrays.sort(xValues);
        int max = 0;
        for (int j = 0; j < xValues.length - 1; j++) {
            if (xValues[j + 1] - xValues[j] > max) {
                max = xValues[j + 1] - xValues[j];
            }
        }
        return max;
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).