Problem
Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.
Example 1:
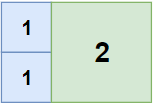
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)
Example 2:
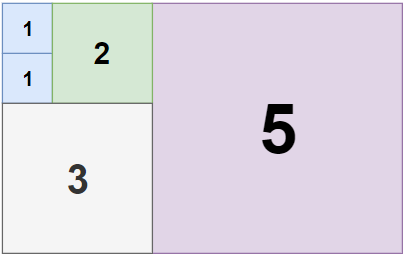
Input: n = 5, m = 8
Output: 5
Example 3:
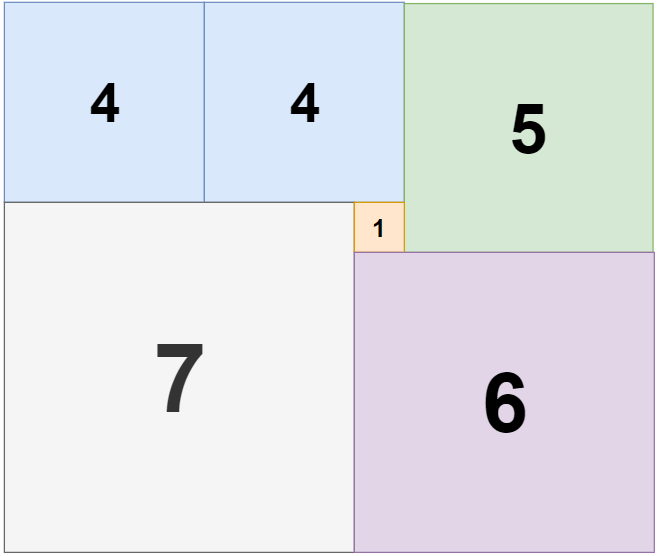
Input: n = 11, m = 13
Output: 6
Constraints:
1 <= n, m <= 13
Solution
class Solution {
private int n;
private int m;
private boolean[][] covered;
private int res;
public int tilingRectangle(int n, int m) {
this.n = n;
this.m = m;
this.covered = new boolean[n][m];
this.res = m * n;
backtrack(0);
return res;
}
private void backtrack(int count) {
if (count >= res) {
return;
}
boolean find = false;
for (int r = 0; r < n; r++) {
for (int c = 0; c < m; c++) {
if (!covered[r][c]) {
find = true;
int len = findMaxWidth(r, c);
while (len > 0) {
cover(r, c, len, true);
backtrack(count + 1);
cover(r, c, len, false);
len--;
}
break;
}
}
if (find) {
break;
}
}
if (!find) {
res = count;
}
}
private void cover(int r, int c, int len, boolean flag) {
for (int i = r; i < r + len; i++) {
for (int j = c; j < c + len; j++) {
covered[i][j] = flag;
}
}
}
private int findMaxWidth(int r, int c) {
int len = Math.min(n - r, m - c);
while (true) {
boolean find = false;
for (int i = r; i < r + len; i++) {
for (int j = c; j < c + len; j++) {
if (covered[i][j]) {
find = true;
len = Math.min(i - r, j - c);
break;
}
}
if (find) {
break;
}
}
if (!find) {
break;
}
}
return len;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).