1022. Sum of Root To Leaf Binary Numbers

Problem

You are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.

• For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.

The test cases are generated so that the answer fits in a 32-bits integer.

  Example 1:

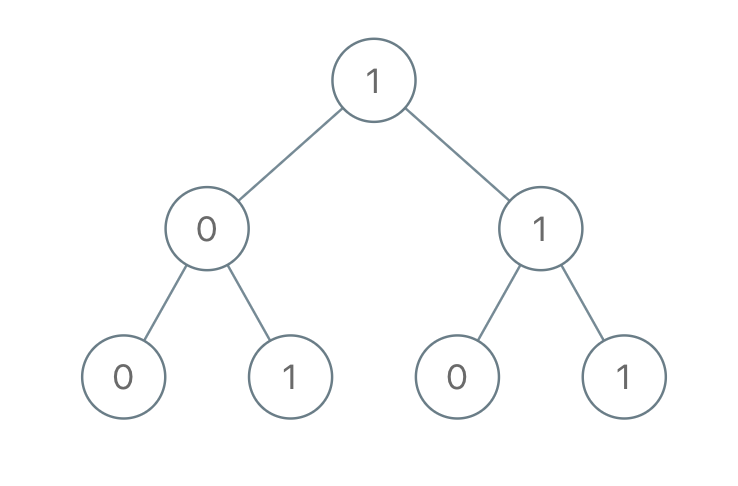
Input: root = [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

Example 2:

Input: root = [0]
Output: 0

  Constraints:

• The number of nodes in the tree is in the range [1, 1000].

• Node.val is 0 or 1.

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumRootToLeaf(TreeNode root) {
        List<List<Integer>> paths = new ArrayList<>();
        dfs(root, paths, new ArrayList<>());
        int sum = 0;
        for (List<Integer> list : paths) {
            int num = 0;
            for (int i : list) {
                num = (num << 1) + i;
            }
            sum += num;
        }
        return sum;
    }

    private void dfs(TreeNode root, List<List<Integer>> paths, List<Integer> path) {
        path.add(root.val);
        if (root.left != null) {
            dfs(root.left, paths, path);
            path.remove(path.size() - 1);
        }
        if (root.right != null) {
            dfs(root.right, paths, path);
            path.remove(path.size() - 1);
        }
        if (root.left == null && root.right == null) {
            paths.add(new ArrayList<>(path));
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).