Problem
You are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.
Return **the *lexicographically smallest* string that starts at a leaf of this tree and ends at the root**.
As a reminder, any shorter prefix of a string is lexicographically smaller.
- For example,
"ab"is lexicographically smaller than"aba".
A leaf of a node is a node that has no children.
Example 1:
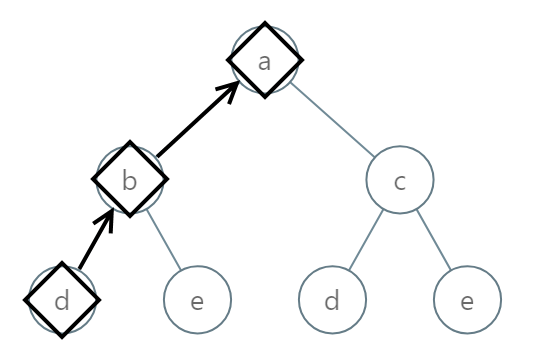
Input: root = [0,1,2,3,4,3,4]
Output: "dba"
Example 2:
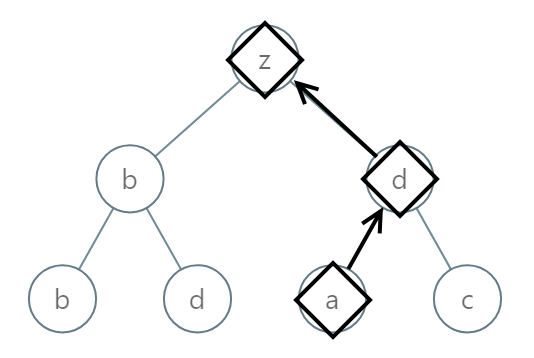
Input: root = [25,1,3,1,3,0,2]
Output: "adz"
Example 3:
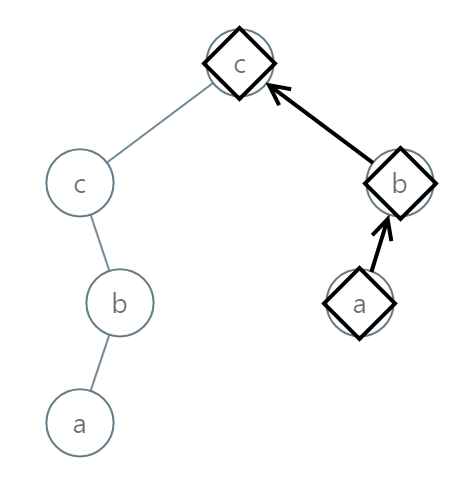
Input: root = [2,2,1,null,1,0,null,0]
Output: "abc"
Constraints:
The number of nodes in the tree is in the range
[1, 8500].0 <= Node.val <= 25
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private String res = "";
public String smallestFromLeaf(TreeNode root) {
dfs(root, new StringBuilder());
return res;
}
private void dfs(TreeNode root, StringBuilder currStr) {
if (root == null) {
return;
}
currStr.insert(0, (char) (root.val + 97));
if (root.left == null && root.right == null) {
if (res.equals("")) {
res = currStr.toString();
} else {
res = res.compareTo(currStr.toString()) > 0 ? currStr.toString() : res;
}
} else {
dfs(root.left, currStr);
dfs(root.right, currStr);
}
currStr.deleteCharAt(0);
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).