2003. Smallest Missing Genetic Value in Each Subtree

Problem

There is a family tree rooted at 0 consisting of n nodes numbered 0 to n - 1. You are given a 0-indexed integer array parents, where parents[i] is the parent for node i. Since node 0 is the root, parents[0] == -1.

There are 10^5 genetic values, each represented by an integer in the inclusive range [1, 10^5]. You are given a 0-indexed integer array nums, where nums[i] is a **distinct **genetic value for node i.

Return **an array *ans* of length n where ans[i] is** **the *smallest* genetic value that is missing from the subtree rooted at node** i.

The subtree rooted at a node x contains node x and all of its descendant nodes.

  Example 1:

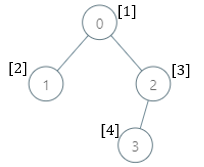
Input: parents = [-1,0,0,2], nums = [1,2,3,4]
Output: [5,1,1,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3] with values [1,2,3,4]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes [2,3] with values [3,4]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.

Example 2:

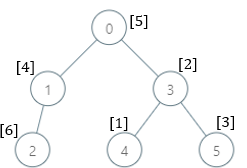
Input: parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
Output: [7,1,1,4,2,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3,4,5] with values [5,4,6,2,1,3]. 7 is the smallest missing value.
- 1: The subtree contains nodes [1,2] with values [4,6]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes [3,4,5] with values [2,1,3]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.

Example 3:

Input: parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
Output: [1,1,1,1,1,1,1]
Explanation: The value 1 is missing from all the subtrees.

  Constraints:

• n == parents.length == nums.length

• 2 <= n <= 10^5

• 0 <= parents[i] <= n - 1 for i != 0

• parents[0] == -1

• parents represents a valid tree.

• 1 <= nums[i] <= 10^5

• Each nums[i] is distinct.

Solution

class Solution {
    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int[] ans = new int[parents.length];
        Node[] all = new Node[parents.length];
        int max = 0;
        for (int i = 0; i < nums.length; i++) {
            all[i] = new Node(i, nums[i]);
            max = Math.max(max, nums[i]);
        }
        for (int i = 1; i < parents.length; i++) {
            all[parents[i]].nodes.add(all[i]);
        }
        solve(all[0], ans, new UF(++max, nums));
        return ans;
    }

    private void solve(Node root, int[] ans, UF uf) {
        int max = 1;
        for (Node child : root.nodes) {
            solve(child, ans, uf);
            uf.union(root.val, child.val);
            max = Math.max(ans[child.idx], max);
        }
        while (max <= ans.length && uf.isConnected(max, root.val)) {
            ++max;
        }
        ans[root.idx] = max;
    }

    private static class Node {
        int idx;
        int val;
        List<Node> nodes;

        Node(int idx, int val) {
            this.idx = idx;
            this.val = val;
            nodes = new ArrayList<>();
        }
    }

    private static class UF {
        int[] rank;
        int[] parent;

        UF(int n, int[] nums) {
            rank = new int[n];
            parent = new int[n];
            for (int m : nums) {
                parent[m] = m;
            }
        }

        private int find(int x) {
            if (x == parent[x]) {
                return x;
            }
            parent[x] = find(parent[x]);
            return parent[x];
        }

        private void union(int x, int y) {
            x = find(x);
            y = find(y);
            if (rank[x] > rank[y]) {
                parent[y] = x;
            } else {
                parent[x] = y;
                if (rank[x] == rank[y]) {
                    rank[y]++;
                }
            }
        }

        private boolean isConnected(int x, int y) {
            return find(x) == find(y);
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).