864. Shortest Path to Get All Keys

Problem

You are given an m x n grid grid where:

• '.' is an empty cell.

• '#' is a wall.

• '@' is the starting point.

• Lowercase letters represent keys.

• Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

  Example 1:

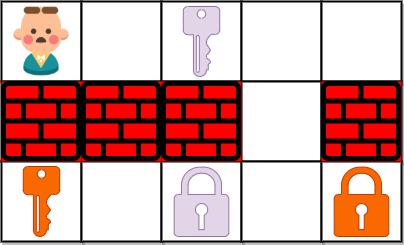
Input: grid = ["@.a..","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

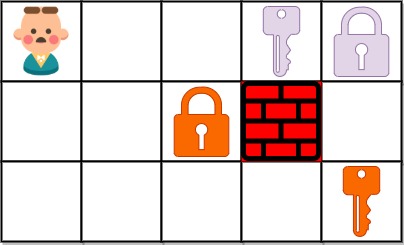
Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 30

• grid[i][j] is either an English letter, '.', '#', or '@'.

• The number of keys in the grid is in the range [1, 6].

• Each key in the grid is unique.

• Each key in the grid has a matching lock.

Solution

class Solution {
    private int m;
    private int n;

    public int shortestPathAllKeys(String[] stringGrid) {
        // strategy: BFS + masking
        m = stringGrid.length;
        n = stringGrid[0].length();
        char[][] grid = new char[m][n];
        int index = 0;
        // convert to char Array
        for (String s : stringGrid) {
            grid[index++] = s.toCharArray();
        }
        // number of keys
        int count = 0;
        Queue<int[]> q = new LinkedList<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // find starting position
                if (grid[i][j] == '@') {
                    q.add(new int[] {i, j, 0});
                }
                // count number of keys
                if ('a' <= grid[i][j] && grid[i][j] <= 'f') {
                    count++;
                }
            }
        }
        int[] dx = {-1, 0, 1, 0};
        int[] dy = {0, -1, 0, 1};
        // this is the amt of keys we need
        int target = (1 << count) - 1;
        // keep track of position and current state
        boolean[][][] visited = new boolean[m][n][target + 1];
        // set initial position and state to true
        visited[q.peek()[0]][q.peek()[1]][0] = true;
        int steps = 0;
        while (!q.isEmpty()) {
            // use size to make sure everything is on one level
            int size = q.size();
            while (--size >= 0) {
                int[] curr = q.poll();
                int x = curr[0];
                int y = curr[1];
                int state = curr[2];
                // found all keys
                if (state == target) {
                    return steps;
                }
                for (int i = 0; i < 4; i++) {
                    int nx = x + dx[i];
                    int ny = y + dy[i];
                    // use new state so we don't mess up current state
                    int nState = state;
                    // out of bounds or reached wall
                    if (!inBounds(nx, ny) || grid[nx][ny] == '#') {
                        continue;
                    }
                    // found key
                    // use OR to add key to our current state because if we already had the key the
                    // digit would still be 1/true
                    if ('a' <= grid[nx][ny] && grid[nx][ny] <= 'f') {
                        // bit mask our found key
                        nState = state | (1 << (grid[nx][ny] - 'a'));
                    }
                    // found lock
                    // use & to see if we have the key
                    // 0 means that the digit we are looking at is 0
                    // need a 1 at the digit spot which means there is a key there
                    if (('A' > grid[nx][ny]
                                    || grid[nx][ny] > 'F'
                                    || ((nState & (1 << (grid[nx][ny] - 'A'))) != 0))
                            && !visited[nx][ny][nState]) {
                        q.add(new int[] {nx, ny, nState});
                        visited[nx][ny][nState] = true;
                    }
                }
            }
            steps++;
        }
        return -1;
    }

    private boolean inBounds(int x, int y) {
        return x >= 0 && x < m && y >= 0 && y < n;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).