Shortest Cycle in a Graph - LeetCode solutions

Problem

There is a **bi-directional **graph with n vertices, where each vertex is labeled from 0 to n - 1. The edges in the graph are represented by a given 2D integer array edges, where edges[i] = [ui, vi] denotes an edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

Return **the length of the **shortest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.

Example 1:

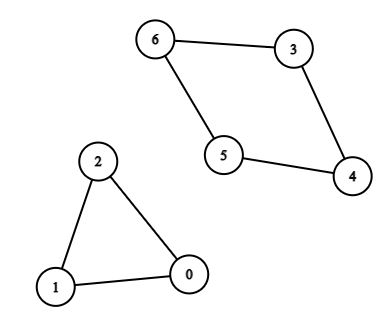
Input: n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
Output: 3
Explanation: The cycle with the smallest length is : 0 -> 1 -> 2 -> 0

Example 2:

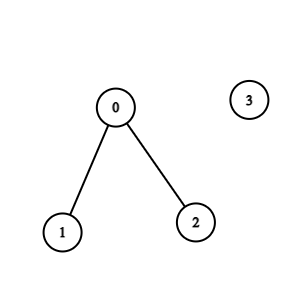
Input: n = 4, edges = [[0,1],[0,2]]
Output: -1
Explanation: There are no cycles in this graph.

Constraints:

2 <= n <= 1000
1 <= edges.length <= 1000
edges[i].length == 2
0 <= ui, vi < n
ui != vi
There are no repeated edges.

Solution (Java)

class Solution  {
      public int findShortestCycle(int n, int[][] edges) {
        List<Integer>[] adj = new List[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            adj[u].add(v);
            adj[v].add(u);
        }

        int minCycle = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            int[] dist = new int[n];
            Arrays.fill(dist, -1);
            Queue<Integer> queue = new LinkedList<>();
            queue.offer(i);
            dist[i] = 0;
            while (!queue.isEmpty()) {
                int u = queue.poll();
                for (int v : adj[u]) {
                    if (dist[v] == -1) {
                        dist[v] = dist[u] + 1;
                        queue.offer(v);
                    } else if (v != i && dist[v] >= dist[u]) {
                        minCycle = Math.min(minCycle, dist[u] + dist[v] + 1);
                    }
                }
            }
        }

        return minCycle == Integer.MAX_VALUE ? -1 : minCycle;
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).