Reverse Odd Levels of Binary Tree

Problem

Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.

For example, suppose the node values at level 3 are [2,1,3,4,7,11,29,18], then it should become [18,29,11,7,4,3,1,2].

Return the root of the reversed tree.

A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.

The level of a node is the number of edges along the path between it and the root node.

Example 1:

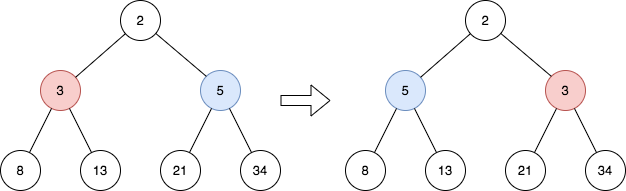
Input: root = [2,3,5,8,13,21,34]
Output: [2,5,3,8,13,21,34]
Explanation: 
The tree has only one odd level.
The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.

Example 2:

Input: root = [7,13,11]
Output: [7,11,13]
Explanation: 
The nodes at level 1 are 13, 11, which are reversed and become 11, 13.

Example 3:

Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
Explanation: 
The odd levels have non-zero values.
The nodes at level 1 were 1, 2, and are 2, 1 after the reversal.
The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.

Constraints:

The number of nodes in the tree is in the range [1, 214].
0 <= Node.val <= 10^5
root is a perfect binary tree.

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode reverseOddLevels(TreeNode root) {
        if(root == null)
            return root;

        Queue<TreeNode> queue = new LinkedList<>();
        int level = 0;

        queue.add(root);

        while (!queue.isEmpty()) {
            int size = queue.size();
            level++;

            TreeNode[] arr = new TreeNode[size];

            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                arr[i] = cur;

                if(cur.left != null){
                    queue.add(cur.left);
                    queue.add(cur.right);
                }
            }

            if (level % 2 == 0) {
                int left = 0;
                int right = size - 1;

                while (left < right) {
                    int leftVal = arr[left].val;
                    arr[left].val = arr[right].val;
                    arr[right].val = leftVal;

                    left++;
                    right--;
                }
            }
        }

        return root;
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).