685. Redundant Connection II

Problem

In this problem, a rooted tree is a directed graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.

The given input is a directed graph that started as a rooted tree with n nodes (with distinct values from 1 to n), with one additional directed edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed.

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [ui, vi] that represents a directed edge connecting nodes ui and vi, where ui is a parent of child vi.

Return an edge that can be removed so that the resulting graph is a rooted tree of n nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array.

  Example 1:

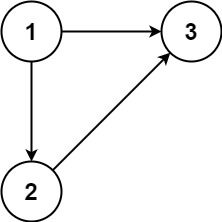
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

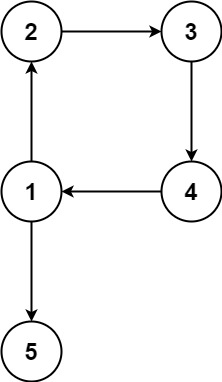
Input: edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
Output: [4,1]

  Constraints:

• n == edges.length

• 3 <= n <= 1000

• edges[i].length == 2

• 1 <= ui, vi <= n

• ui != vi

Solution

class Solution {
    public int[] findRedundantDirectedConnection(int[][] edges) {
        int n = edges.length;

        int[] roots = new int[n + 1];
        for (int i = 0; i < n + 1; i++) roots[i] = i;

        int[] candidate1 = null, candidate2 = null;

        for (int[] edge : edges){
            int from = edge[0], to = edge[1];
            int rootOfFromNode = findRoot(roots, from);
            int rootOfToNode = findRoot(roots, to);

            // when an issue happens, we skip the "union" process

            // record the last edge which results in "2 parents" issue
            if (rootOfToNode != to) candidate1 = edge; 
            // record the last edge which results in "cycle" issue, if any
            else if (rootOfFromNode == rootOfToNode) candidate2 = edge; 
            // no issue happened, we can union now
            else roots[rootOfToNode] = rootOfFromNode;
        }

        // If there is only one issue, return this one.
        if (candidate1 == null) return candidate2; 
        if (candidate2 == null) return candidate1;

        /* If both issues present, then the answer should be the first edge which results in "2 parents" issue
        The reason is, when an issue happens, we skip the "union" process.
    Therefore, if both issues happen, it means the incorrent edge which results in "2 parents" was ignored. */
        for (int[] edge : edges) {
            int to = edge[1];
            if (to == candidate1[1]) return edge;
        }

        return new int[]{0, 0};
    }

    private int findRoot(int[] roots, int i){
        int node = i;
        while (node != roots[node]){
            int parent = roots[node];
            node = parent;
        }
        return node;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).