2368. Reachable Nodes With Restrictions

Problem

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return **the *maximum* number of nodes you can reach from node 0 without visiting a restricted node.**

Note that node 0 will not be a restricted node.

  Example 1:

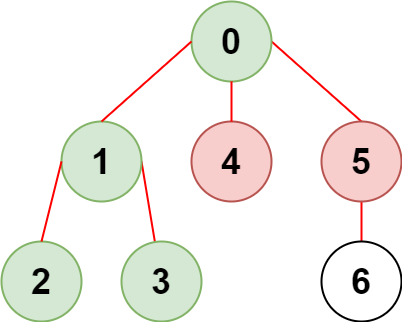
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

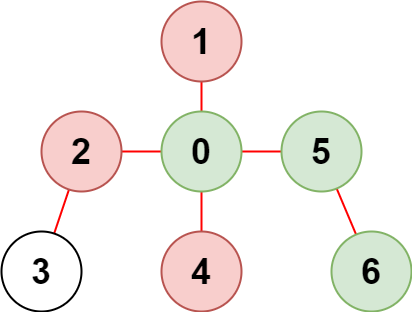
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

  Constraints:

• 2 <= n <= 10^5

• edges.length == n - 1

• edges[i].length == 2

• 0 <= ai, bi < n

• ai != bi

• edges represents a valid tree.

• 1 <= restricted.length < n

• 1 <= restricted[i] < n

• All the values of restricted are unique.

Solution (Java)

class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int src = edge[0];
            int dest = edge[1];
            graph[src].add(dest);
            graph[dest].add(src);
        }
        Queue<Integer> q = new ArrayDeque<>();
        boolean[] visited = new boolean[n];
        q.offer(0);
        visited[0] = true;
        for (int node : restricted) {
            visited[node] = true;
        }
        int ans = 0;
        while (!q.isEmpty()) {
            int vertex = q.poll();
            ans++;
            for (int neighbour : graph[vertex]) {
                if (!visited[neighbour]) {
                    q.offer(neighbour);
                    visited[neighbour] = true;
                }
            }
        }
        return ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).