938. Range Sum of BST

Problem

Given the root node of a binary search tree and two integers low and high, return **the sum of values of all nodes with a value in the *inclusive* range **[low, high].

  Example 1:

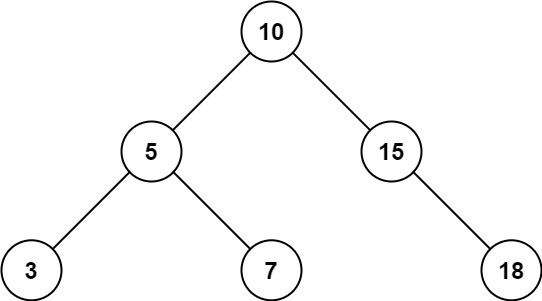
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2:

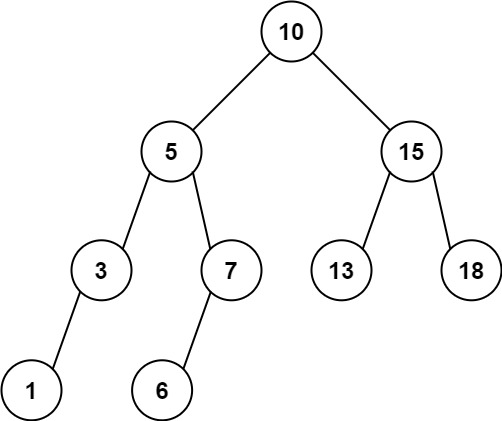
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

  Constraints:

• The number of nodes in the tree is in the range [1, 2 * 10^4].

• 1 <= Node.val <= 10^5

• 1 <= low <= high <= 10^5

• All Node.val are unique.

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rangeSumBST(TreeNode root, int low, int high) {
        if (root == null) {
            return 0;
        }
        if (root.val <= high && root.val >= low) {
            int sum = root.val;
            int left = rangeSumBST(root.left, low, high);
            int right = rangeSumBST(root.right, low, high);
            return sum + left + right;
        } else if (root.val < low) {
            return rangeSumBST(root.right, low, high);
        } else {
            return rangeSumBST(root.left, low, high);
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).