Problem
You are given an m x n matrix M initialized with all 0's and an array of operations ops, where ops[i] = [ai, bi] means M[x][y] should be incremented by one for all 0 <= x < ai and 0 <= y < bi.
Count and return the number of maximum integers in the matrix after performing all the operations.
Example 1:
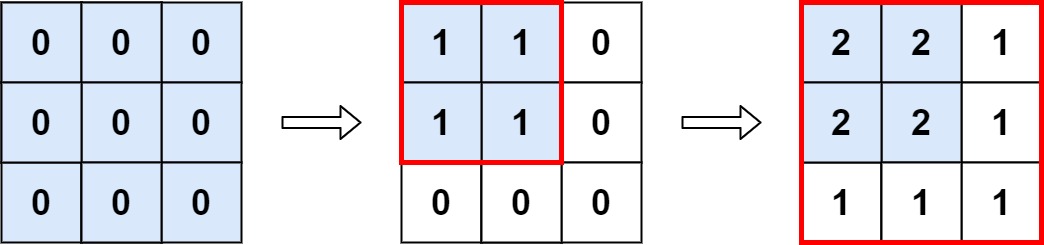
Input: m = 3, n = 3, ops = [[2,2],[3,3]]
Output: 4
Explanation: The maximum integer in M is 2, and there are four of it in M. So return 4.
Example 2:
Input: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
Output: 4
Example 3:
Input: m = 3, n = 3, ops = []
Output: 9
Constraints:
1 <= m, n <= 4 * 10^40 <= ops.length <= 10^4ops[i].length == 21 <= ai <= m1 <= bi <= n
Solution (Java)
class Solution {
/*
* Since the incrementing starts from zero to op[0] and op[1], we only need to find the range that
* has the most overlaps. Thus we keep finding the minimum of both x and y.
*/
public int maxCount(int m, int n, int[][] ops) {
int x = m;
int y = n;
for (int[] op : ops) {
x = Math.min(x, op[0]);
y = Math.min(y, op[1]);
}
return x * y;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).