Problem
Given a string path, where path[i] = 'N', 'S', 'E' or 'W', each representing moving one unit north, south, east, or west, respectively. You start at the origin (0, 0) on a 2D plane and walk on the path specified by path.
Return true if the path crosses itself at any point, that is, if at any time you are on a location you have previously visited. Return false otherwise.
Example 1:
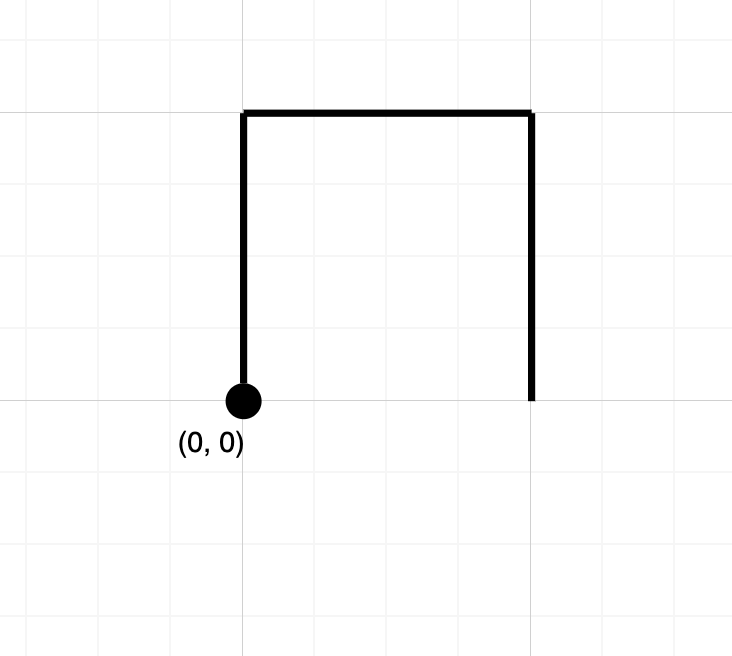
Input: path = "NES"
Output: false
Explanation: Notice that the path doesn't cross any point more than once.
Example 2:
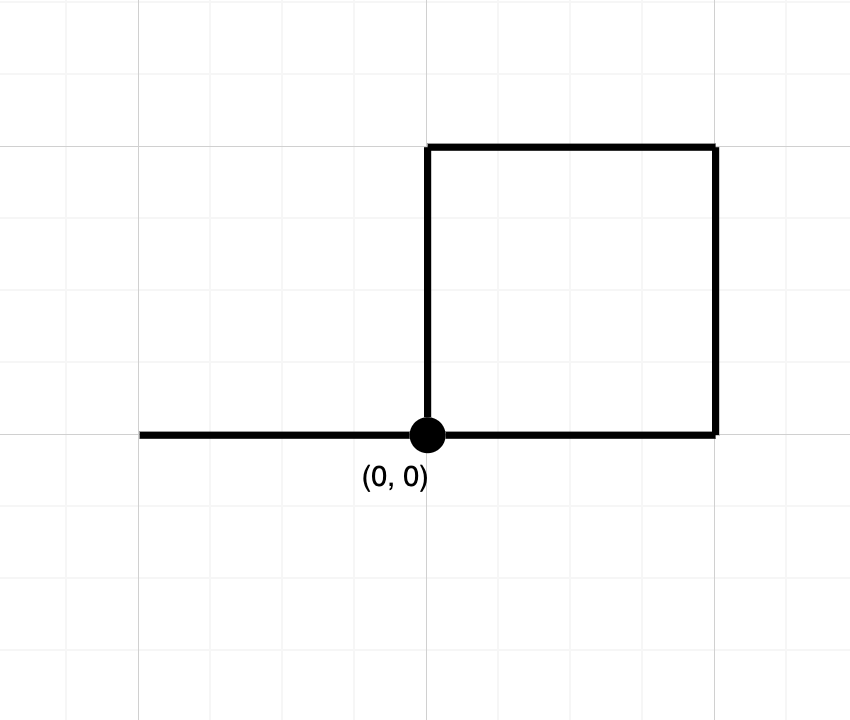
Input: path = "NESWW"
Output: true
Explanation: Notice that the path visits the origin twice.
Constraints:
1 <= path.length <= 10^4path[i]is either'N','S','E', or'W'.
Solution (Java)
class Solution {
public boolean isPathCrossing(String path) {
Set<String> visited = new HashSet<String>();
int x = 0, y = 0;
for(char ch: path.toCharArray()) {
visited.add(getKey(x,y));
x += getX(ch);
y += getY(ch);
//System.out.printf("%d, %d\n", x, y);
if(visited.contains(getKey(x,y))) {
return true;
}
}
return false;
}
private String getKey(int x, int y) {
return x + "," + y;
}
private int getX(char ch) {
if(ch == 'N' || ch =='S') return 0;
if(ch =='E') return -1;
if(ch == 'W') return +1;
return 0;
}
private int getY(char ch) {
if(ch == 'E' || ch == 'W') return 0;
if(ch =='S') return -1;
if(ch == 'N') return +1;
return 0;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).