Problem
You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 10^9 + 7.
Example 1:
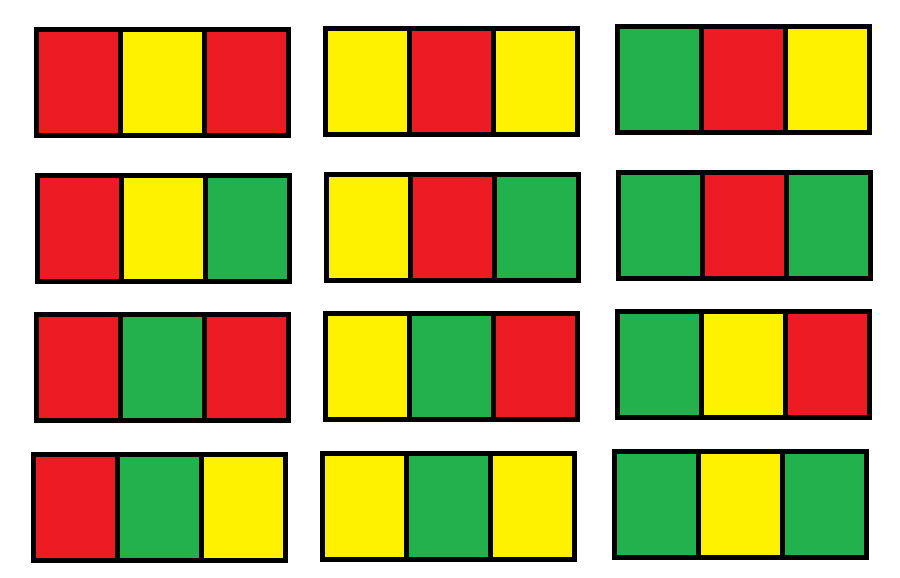
Input: n = 1
Output: 12
Explanation: There are 12 possible way to paint the grid as shown.
Example 2:
Input: n = 5000
Output: 30228214
Constraints:
n == grid.length1 <= n <= 5000
Solution
class Solution {
private static final int MOD = 1000000007;
public int numOfWays(int n) {
int[][] dp = new int[n + 1][12];
Arrays.fill(dp[1], 1);
int[][] transfer =
new int[][] {
{5, 6, 8, 9, 10},
{5, 8, 7, 9, -1},
{5, 6, 9, 10, 12},
{6, 10, 11, 12, -1},
{1, 2, 3, 11, 12},
{1, 3, 4, 11, -1},
{2, 9, 10, 12, -1},
{1, 2, 10, 11, 12},
{1, 2, 3, 7, -1},
{1, 3, 4, 7, 8},
{4, 5, 6, 8, -1},
{3, 4, 5, 7, 8}
};
for (int i = 2; i <= n; i++) {
for (int j = 0; j < 12; j++) {
int[] prevStates = transfer[j];
int sum = 0;
for (int s : prevStates) {
if (s == -1) {
break;
}
sum = (sum + dp[i - 1][s - 1]) % MOD;
}
dp[i][j] = sum;
}
}
int total = 0;
for (int i = 0; i < 12; i++) {
total = (total + dp[n][i]) % MOD;
}
return total;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).