Number of Different Subsequences GCDs

Problem

You are given an array nums that consists of positive integers.

The GCD of a sequence of numbers is defined as the greatest integer that divides all the numbers in the sequence evenly.

For example, the GCD of the sequence [4,6,16] is 2.

A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array.

For example, [2,5,10] is a subsequence of [1,2,1,**2**,4,1,**5**,**10**].

Return **the *number* of different GCDs among all non-empty subsequences of** nums.

Example 1:

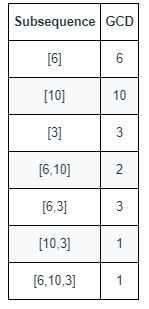
Input: nums = [6,10,3]
Output: 5
Explanation: The figure shows all the non-empty subsequences and their GCDs.
The different GCDs are 6, 10, 3, 2, and 1.

Example 2:

Input: nums = [5,15,40,5,6]
Output: 7

Constraints:

1 <= nums.length <= 10^5
1 <= nums[i] <= 2 * 10^5

Solution

class Solution {
    public int countDifferentSubsequenceGCDs(int[] nums) {
        int max = 0;
        for (int num : nums) {
            max = Math.max(max, num);
        }
        boolean[] present = new boolean[200001];
        for (int num : nums) {
            max = Math.max(max, num);
            present[num] = true;
        }
        int count = 0;
        for (int i = 1; i <= max; i++) {
            if (present[i]) {
                count++;
                continue;
            }
            int tempGcd = 0;
            for (int j = i; j <= max; j += i) {
                if (present[j]) {
                    tempGcd = gcd(tempGcd, j);
                }
                if (tempGcd == i) {
                    count++;
                    break;
                }
            }
        }
        return count;
    }

    private int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).