2374. Node With Highest Edge Score

Problem

You are given a directed graph with n nodes labeled from 0 to n - 1, where each node has exactly one outgoing edge.

The graph is represented by a given 0-indexed integer array edges of length n, where edges[i] indicates that there is a directed edge from node i to node edges[i].

The edge score of a node i is defined as the sum of the labels of all the nodes that have an edge pointing to i.

Return **the node with the highest *edge score***. If multiple nodes have the same *edge score*, return the node with the *smallest* index.

  Example 1:

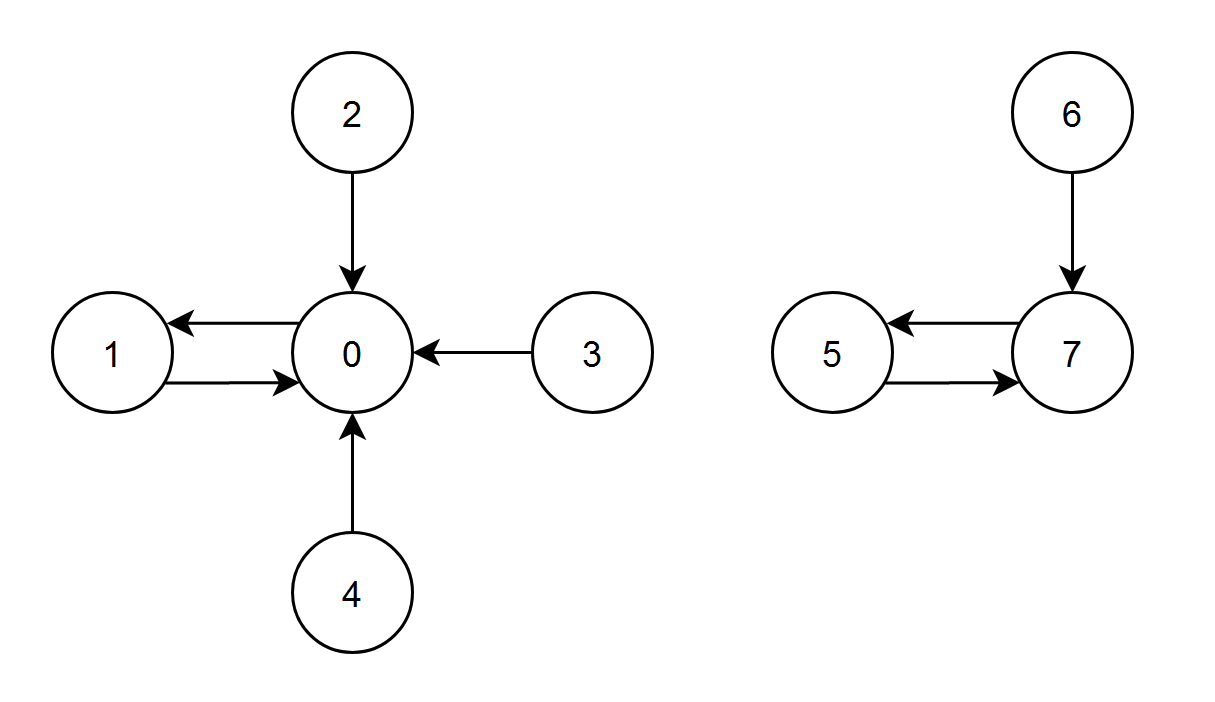
Input: edges = [1,0,0,0,0,7,7,5]
Output: 7
Explanation:
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.

Example 2:

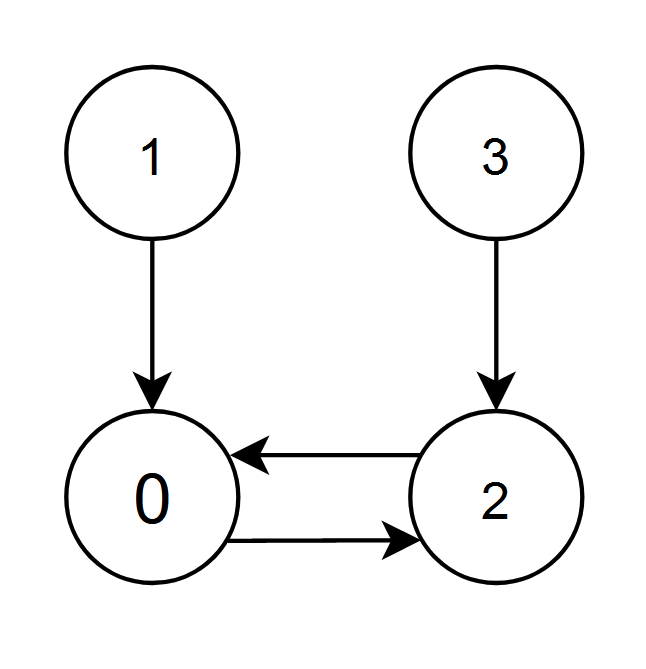
Input: edges = [2,0,0,2]
Output: 0
Explanation:
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.

  Constraints:

• n == edges.length

• 2 <= n <= 10^5

• 0 <= edges[i] < n

• edges[i] != i

Solution (Java)

class Solution {
    public int edgeScore(int[] edges) {
        int n = edges.length;
        int[] score = new int[n];
        int maxScore = 0;
        int node = 0;
        for (int i = 0; i < n; i++) {
            score[edges[i]] += i;
            if (score[edges[i]] >= maxScore) {
                if (score[edges[i]] == maxScore) {
                    node = Math.min(node, edges[i]);
                } else {
                    node = edges[i];
                }
                maxScore = score[edges[i]];
            }
        }
        return node;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).