1560. Most Visited Sector in a Circular Track

Problem

Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The ith round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]

Return an array of the most visited sectors sorted in ascending order.

Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).

  Example 1:

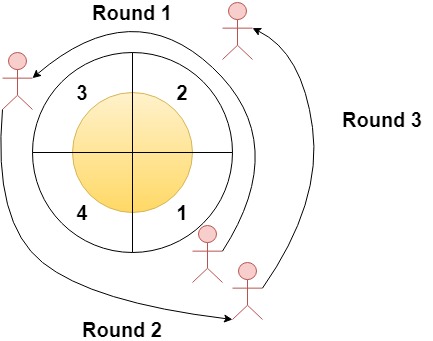
Input: n = 4, rounds = [1,3,1,2]
Output: [1,2]
Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.

Example 2:

Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2]
Output: [2]

Example 3:

Input: n = 7, rounds = [1,3,5,7]
Output: [1,2,3,4,5,6,7]

  Constraints:

• 2 <= n <= 100

• 1 <= m <= 100

• rounds.length == m + 1

• 1 <= rounds[i] <= n

• rounds[i] != rounds[i + 1] for 0 <= i < m

Solution (Java)

class Solution {
    public List<Integer> mostVisited(int n, int[] rounds) {
        List<Integer> res = new ArrayList<>();
        int start = rounds[0];
        int end = rounds[rounds.length - 1];
        int[] ans = new int[n + 1];
        while (start != end) {
            ans[start]++;
            start++;
            if (start > n) {
                start = 1;
            }
        }
        ans[end]++;
        for (int i = 1; i <= n; i++) {
            if (ans[i] != 0) {
                res.add(i);
            }
        }
        return res;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).