Problem
There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.
The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.
All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.
At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.
Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.
Note that
All robots move at the same speed.
If two robots move in the same direction, they will never collide.
If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
If the robot moved from a position
xto a positiony, the distance it moved is|y - x|.
Example 1:
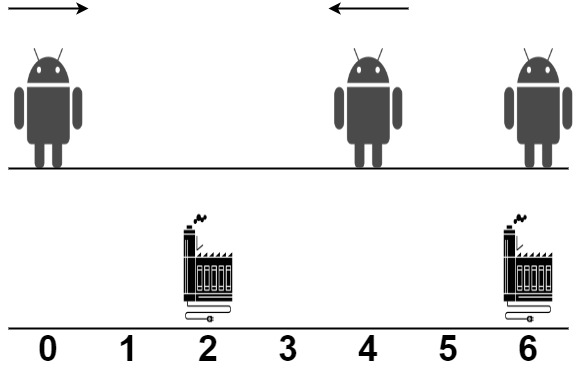
Input: robot = [0,4,6], factory = [[2,2],[6,2]]
Output: 4
Explanation: As shown in the figure:
- The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
- The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
- The third robot at position 6 will be repaired at the second factory. It does not need to move.
The limit of the first factory is 2, and it fixed 2 robots.
The limit of the second factory is 2, and it fixed 1 robot.
The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.
Example 2:
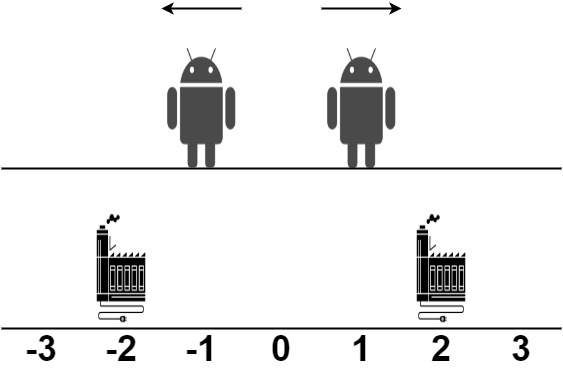
Input: robot = [1,-1], factory = [[-2,1],[2,1]]
Output: 2
Explanation: As shown in the figure:
- The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
- The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
The limit of the first factory is 1, and it fixed 1 robot.
The limit of the second factory is 1, and it fixed 1 robot.
The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.
Constraints:
1 <= robot.length, factory.length <= 100factory[j].length == 2-109 <= robot[i], positionj <= 1090 <= limitj <= robot.lengthThe input will be generated such that it is always possible to repair every robot.
Solution (Java)
class Solution {
public long minimumTotalDistance(List<Integer> robot, int[][] f) {
// sort factories :
// 1. move all factories with 0-capacity to the end
// 2. sort everything else by x-position in asc order
Arrays.sort(f, (a, b) -> (a[1] == 0) ? 1 : (b[1] == 0) ? -1 : a[0] - b[0]);
// Sort robots by x-position in asc order
// As we don't know the implementation of the List that is passed, it is better to map it to an array explicitly
int[] r = new int[robot.size()];
int i = 0;
for (int x : robot) r[i++] = x;
Arrays.sort(r);
// An array to be used for tracking robots assigned to each factory
int[][] d = new int[f.length][2];
// For each robot starting from the rightmost find the most optimal destination factory
// and add it's cost to the result.
long res = 0;
for (i = r.length - 1; i >= 0; i--) res += pop(d, i, r, f);
return res;
}
long pop(int[][] d, int i, int[] r, int[][] f) {
long cost = Long.MAX_VALUE;
int j;
// try assigning robot to each factory starting from the leftmost
for (j = 0; j < d.length; j++) {
// cost of adding robot to the current factory
long t = Math.abs(r[i] - f[j][0]);
int tj = j;
// if current factory is full calculate the cost of moving the rightmost robot in the factory to the next one
// and add the calculated cost to the current cost.
// repeat the same action until we fit our robots to factories.
while (tj < d.length && d[tj][1] == f[tj][1]) {
// if we faced a factory with 0-capactity or the rightmost factory
// it would mean we reached the end and cannot fit our robot to the current factory
if (d[tj][1] == 0 || tj == d.length-1) {
t = Long.MAX_VALUE;
break;
}
int l = d[tj][0] + d[tj][1] - 1;
t += Math.abs(f[tj+1][0] - r[l]) - Math.abs(f[tj][0] - r[l]);
++tj;
}
// if the cost for adding robot to the current factory is greater than the previous one
// it means that the previous one was the most optimal
if (t > cost) {
break;
}
cost = t;
}
// assign current robot to the previous factory and move any non-fit robots to the right
d[j-1][0] = i;
int tj = j-1;
while (d[tj][1] == f[tj][1]) {
d[tj+1][0] = d[tj][0] + d[tj][1];
++tj;
}
d[tj][1]++;
return cost;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).