1578. Minimum Time to Make Rope Colorful

Problem

Alice has n balloons arranged on a rope. You are given a 0-indexed string colors where colors[i] is the color of the ith balloon.

Alice wants the rope to be colorful. She does not want two consecutive balloons to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it colorful. You are given a 0-indexed integer array neededTime where neededTime[i] is the time (in seconds) that Bob needs to remove the ith balloon from the rope.

Return **the *minimum time* Bob needs to make the rope colorful**.

  Example 1:

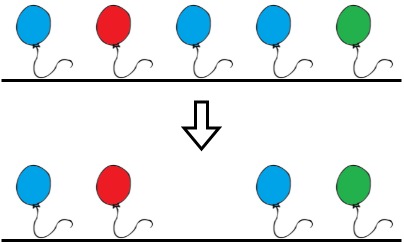
Input: colors = "abaac", neededTime = [1,2,3,4,5]
Output: 3
Explanation: In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.

Example 2:

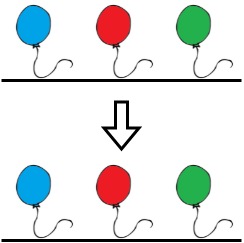
Input: colors = "abc", neededTime = [1,2,3]
Output: 0
Explanation: The rope is already colorful. Bob does not need to remove any balloons from the rope.

Example 3:

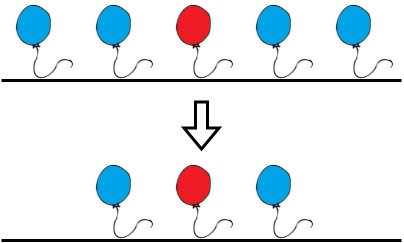
Input: colors = "aabaa", neededTime = [1,2,3,4,1]
Output: 2
Explanation: Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.

  Constraints:

• n == colors.length == neededTime.length

• 1 <= n <= 10^5

• 1 <= neededTime[i] <= 10^4

• colors contains only lowercase English letters.

Solution (Java)

class Solution {
    public int minCost(String s, int[] cost) {
        char[] str = s.toCharArray();
        int minCost = 0;
        for (int i = 1; i < str.length; i++) {
            if (str[i] == str[i - 1]) {
                // accrue the cost of deletion for the lower duplicate
                minCost += Math.min(cost[i], cost[i - 1]);
                // keep the cost of the higher duplicate for next iteration
                cost[i] = Math.max(cost[i], cost[i - 1]);
            }
        }
        return minCost;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).