Minimum Score After Removals on a Tree

Problem

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Remove two distinct edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:

Get the XOR of all the values of the nodes for each of the three components respectively.
The difference between the largest XOR value and the smallest XOR value is the score of the pair.
For example, say the three components have the node values: [4,5,7], [1,9], and [3,3,3]. The three XOR values are 4 ^ 5 ^ 7 = **6**, 1 ^ 9 = **8**, and 3 ^ 3 ^ 3 = **3**. The largest XOR value is 8 and the smallest XOR value is 3. The score is then 8 - 3 = 5.

Return **the *minimum* score of any possible pair of edge removals on the given tree**.

Example 1:

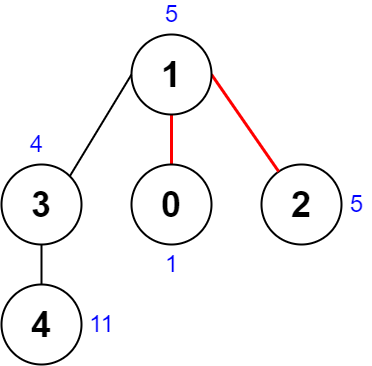
Input: nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
Output: 9
Explanation: The diagram above shows a way to make a pair of removals.
- The 1st component has nodes [1,3,4] with values [5,4,11]. Its XOR value is 5 ^ 4 ^ 11 = 10.
- The 2nd component has node [0] with value [1]. Its XOR value is 1 = 1.
- The 3rd component has node [2] with value [5]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.

Example 2:

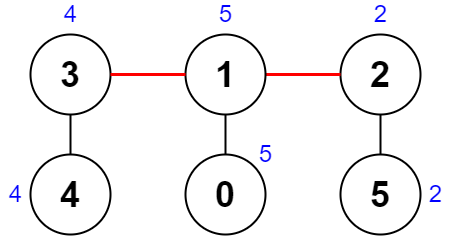
Input: nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
Output: 0
Explanation: The diagram above shows a way to make a pair of removals.
- The 1st component has nodes [3,4] with values [4,4]. Its XOR value is 4 ^ 4 = 0.
- The 2nd component has nodes [1,0] with values [5,5]. Its XOR value is 5 ^ 5 = 0.
- The 3rd component has nodes [2,5] with values [2,2]. Its XOR value is 2 ^ 2 = 0.
The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0.
We cannot obtain a smaller score than 0.

Constraints:

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 10^8
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges represents a valid tree.

Solution

class Solution {
    private int ans = Integer.MAX_VALUE;

    // function to travel 2nd time on the tree and find the second edge to be removed
    private int helper(
            int src, ArrayList<Integer>[] graph, int[] arr, int par, int block, int xor1, int tot) {
        // Setting the value for the current subtree's XOR value
        int myXOR = arr[src];
        for (int nbr : graph[src]) {
            // If the current nbr is niether the parent of this node nor the blocked node  , then
            // only we'll proceed
            if (nbr != par && nbr != block) {
                int nbrXOR = helper(nbr, graph, arr, src, block, xor1, tot);
                // 'src <----> nbr' is the second edge to be removed
                // Getting the XOR value of the current neighbor
                int xor2 = nbrXOR;
                // The XOR of the remaining component
                int xor3 = (tot ^ xor1) ^ xor2;
                // Getting the minimum of the three values
                int max = Math.max(xor1, Math.max(xor2, xor3));
                // Getting the maximum of the three value
                int min = Math.min(xor1, Math.min(xor2, xor3));
                ans = Math.min(ans, max - min);
                // Including the neighbour subtree's XOR value in the XOR value of the subtree
                // rooted at src node
                myXOR ^= nbrXOR;
            }
        }
        // Returing the XOR value of the current subtree rooted at the src node
        return myXOR;
    }

    // function to travel 1st time on the tree and find the first edge to be removed and
    // then block the node at which the edge ends to avoid selecting the same node again
    private int dfs(int src, ArrayList<Integer>[] graph, int[] arr, int par, int tot) {
        // Setting the value for the current subtree's XOR value
        int myXOR = arr[src];
        for (int nbr : graph[src]) {
            // If the current nbr is not the parent of this node, then only we'll proceed
            if (nbr != par) {
                // After selecting 'src <----> nbr' as the first edge, we block 'nbr' node and then
                // make a call to try all the second edges
                int nbrXOR = dfs(nbr, graph, arr, src, tot);
                // Calling the helper to find the try all the second edges after blocking the
                // current node
                helper(0, graph, arr, -1, nbr, nbrXOR, tot);
                // Including the neighbour subtree's XOR value in the XOR value of the subtree
                // rooted at src node
                myXOR ^= nbrXOR;
            }
        }
        // Returing the XOR value of the current subtree rooted at the src node
        return myXOR;
    }

    public int minimumScore(int[] arr, int[][] edges) {
        int n = arr.length;
        ArrayList<Integer>[] graph = new ArrayList[n];
        int tot = 0;
        for (int i = 0; i < n; i++) {
            // Initializing the graph and finding the total XOR
            graph[i] = new ArrayList<>();
            tot ^= arr[i];
        }
        for (int[] edge : edges) {
            // adding the edges
            int u = edge[0];
            int v = edge[1];
            graph[u].add(v);
            graph[v].add(u);
        }
        ans = Integer.MAX_VALUE;
        dfs(0, graph, arr, -1, tot);
        return ans;
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).