2471. Minimum Number of Operations to Sort a Binary Tree by Level

Problem

You are given the root of a binary tree with unique values.

In one operation, you can choose any two nodes at the same level and swap their values.

Return **the minimum number of operations needed to make the values at each level sorted in a *strictly increasing order***.

The level of a node is the number of edges along the path between it and the root node.

  Example 1:

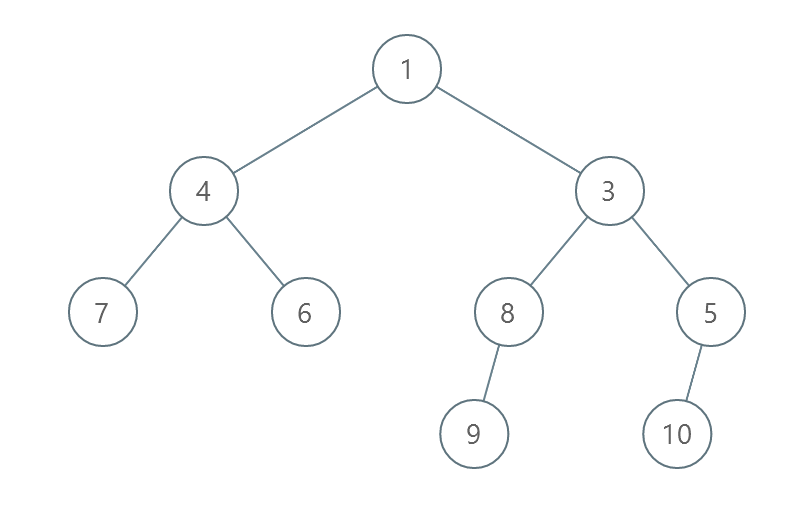
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
Output: 3
Explanation:
- Swap 4 and 3. The 2nd level becomes [3,4].
- Swap 7 and 5. The 3rd level becomes [5,6,8,7].
- Swap 8 and 7. The 3rd level becomes [5,6,7,8].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.

Example 2:

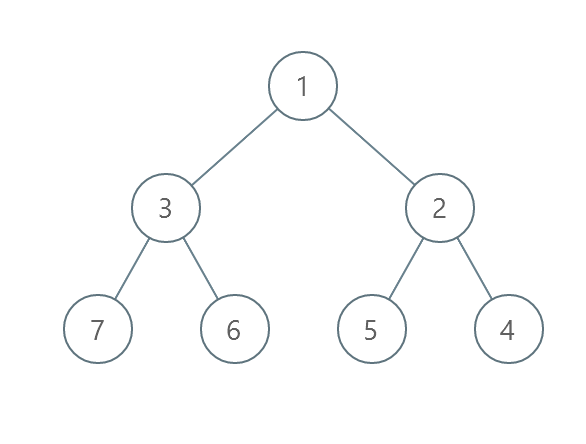
Input: root = [1,3,2,7,6,5,4]
Output: 3
Explanation:
- Swap 3 and 2. The 2nd level becomes [2,3].
- Swap 7 and 4. The 3rd level becomes [4,6,5,7].
- Swap 6 and 5. The 3rd level becomes [4,5,6,7].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.

Example 3:

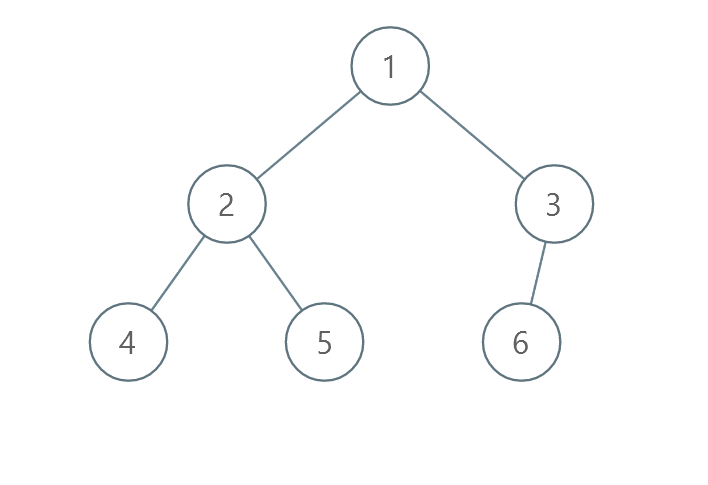
Input: root = [1,2,3,4,5,6]
Output: 0
Explanation: Each level is already sorted in increasing order so return 0.

  Constraints:

• The number of nodes in the tree is in the range [1, 105].

• 1 <= Node.val <= 105

• All the values of the tree are unique.

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minimumOperations(TreeNode root) {
        Queue<TreeNode> nm=new LinkedList<>();
        nm.offer(root);
        int s=0;
        while(!nm.isEmpty())
        {
            int m=0,l=nm.size();
            List<Integer> kk=new ArrayList<>();
            for(int i=0;i<l;i++)
            {
                if(nm.peek().left!=null)
                {
                    nm.add(nm.peek().left);
                }
                if(nm.peek().right!=null)
                {
                    nm.add(nm.peek().right);
                }
                int f=nm.poll().val;
                kk.add(f);
            }
            s+=task(kk);
        }
        return s;
    }
    public int task(List<Integer> nm)
    {
        Map<Integer,Integer> kk=new HashMap<>();
        for(int i=0;i<nm.size();i++)
        {
            kk.put(nm.get(i),i);
        }
        Collections.sort(nm);
        boolean k[]=new boolean[nm.size()];
        int s=0;
        for(int i=0;i<nm.size();i++)
        {
            if(k[i] || kk.get(nm.get(i))==i)
            {
                continue;
            }
            int j=i,m=0;
            while(!k[j])
            {
                k[j]=true;
                j=kk.get(nm.get(j));
                m++;
            }
            if(m>0)
            {
                s+=m-1;
            }
        }
        return s;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).