2858. Minimum Edge Reversals So Every Node Is Reachable

Problem

There is a simple directed graph with n nodes labeled from 0 to n - 1. The graph would form a tree if its edges were bi-directional.

You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.

An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.

For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

Return **an integer array *answer*, where *answer[i]* is the**** ** **minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.**

Example 1:

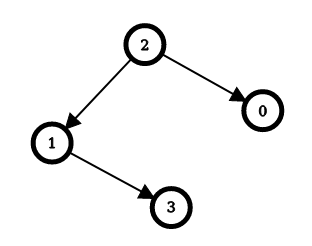
Input: n = 4, edges = [[2,0],[2,1],[1,3]]
Output: [1,1,0,2]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0.
So, answer[0] = 1.
For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1.
So, answer[1] = 1.
For node 2: it is already possible to reach any other node starting from node 2.
So, answer[2] = 0.
For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3.
So, answer[3] = 2.

Example 2:

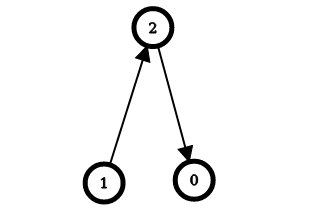
Input: n = 3, edges = [[1,2],[2,0]]
Output: [2,0,1]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0.
So, answer[0] = 2.
For node 1: it is already possible to reach any other node starting from node 1.
So, answer[1] = 0.
For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2.
So, answer[2] = 1.

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ui == edges[i][0] < n
• 0 <= vi == edges[i][1] < n
• ui != vi
• The input is generated such that if the edges were bi-directional, the graph would be a tree.

Solution (Java)

class Solution {
    Map<Integer, Map<Integer, Integer>> G = new HashMap<>();
    int[] res;

    public int[] minEdgeReversals(int n, int[][] edges) {
        G.clear();
        for (int[] e : edges) {
            G.computeIfAbsent(e[0], x -> new HashMap<>()).put(e[1], 0);
            G.computeIfAbsent(e[1], x -> new HashMap<>()).put(e[0], 1);
        }

        res = new int[n];
        Arrays.fill(res, -1);

        dfs(0, dp(-1, 0));
        return res;
    }

    private int dp(int i, int j) {
        int sum = 0;
        for (Integer k : G.get(j).keySet()) {
            if (k == i) continue;
            sum += dp(j, k) + G.get(j).get(k);
        }
        return sum;
    }

    private void dfs(int i, int v) {
        res[i] = v;
        for (Integer j : G.get(i).keySet())
            if (res[j] < 0)
                dfs(j, v - G.get(i).get(j) + G.get(j).get(i));
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).