Problem
You are given n BST (binary search tree) root nodes for n separate BSTs stored in an array trees (0-indexed). Each BST in trees has at most 3 nodes, and no two roots have the same value. In one operation, you can:
Select two distinct indices
iandjsuch that the value stored at one of the **leaves **oftrees[i]is equal to the root value oftrees[j].Replace the leaf node in
trees[i]withtrees[j].Remove
trees[j]fromtrees.
Return** the root of the resulting BST if it is possible to form a valid BST after performing n - 1 operations, or**** **null *if it is impossible to create a valid BST*.
A BST (binary search tree) is a binary tree where each node satisfies the following property:
Every node in the node's left subtree has a value strictly less than the node's value.
Every node in the node's right subtree has a value strictly greater than the node's value.
A leaf is a node that has no children.
Example 1:
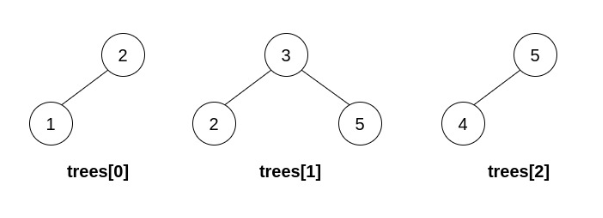
Input: trees = [[2,1],[3,2,5],[5,4]]
Output: [3,2,5,1,null,4]
Explanation:
In the first operation, pick i=1 and j=0, and merge trees[0] into trees[1].
Delete trees[0], so trees = [[3,2,5,1],[5,4]].
In the second operation, pick i=0 and j=1, and merge trees[1] into trees[0].
Delete trees[1], so trees = [[3,2,5,1,null,4]].
The resulting tree, shown above, is a valid BST, so return its root.
Example 2:
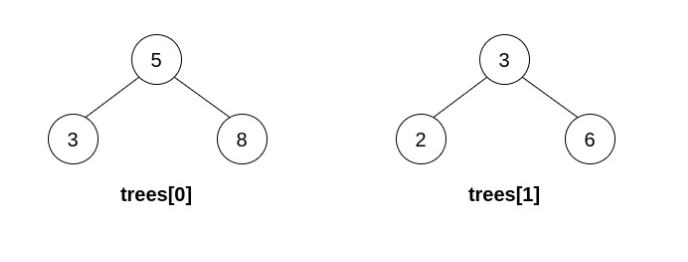
Input: trees = [[5,3,8],[3,2,6]]
Output: []
Explanation:
Pick i=0 and j=1 and merge trees[1] into trees[0].
Delete trees[1], so trees = [[5,3,8,2,6]].
The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null.
Example 3:
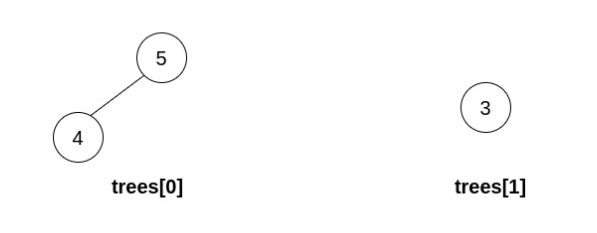
Input: trees = [[5,4],[3]]
Output: []
Explanation: It is impossible to perform any operations.
Constraints:
n == trees.length1 <= n <= 5 * 10^4The number of nodes in each tree is in the range
[1, 3].Each node in the input may have children but no grandchildren.
No two roots of
treeshave the same value.All the trees in the input are valid BSTs.
1 <= TreeNode.val <= 5 * 10^4.
Solution
import java.util.ArrayDeque;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Queue;
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode canMerge(List<TreeNode> trees) {
Map<Integer, TreeNode> valRootMap = new HashMap<Integer, TreeNode>();
Map<TreeNode, int[]> minMaxMap = new HashMap<TreeNode, int[]>();
Map<TreeNode, int[]> legalRangeMap = new HashMap<TreeNode, int[]>();
for (TreeNode root : trees) {
valRootMap.put(root.val, root);
getMinMax(minMaxMap, root);
getLegalRange(legalRangeMap, root, Integer.MIN_VALUE, Integer.MAX_VALUE);
}
Map<Integer, Integer> leavesCountMap = new HashMap<Integer, Integer>();
for (TreeNode tree : trees)
visitLeaves(leavesCountMap, tree, true);
for (Map.Entry<Integer, Integer> entry : leavesCountMap.entrySet()) {
if (entry.getValue() > 1)
return null;
}
Set<TreeNode> set = new HashSet<TreeNode>(trees);
for (TreeNode root : trees) {
if (isLeaf(root))
continue;
TreeNode parent = getLeafParent(root);
TreeNode left = parent.left, right = parent.right;
if (left != null && valRootMap.containsKey(left.val)) {
int[] legalRange = legalRangeMap.get(left);
TreeNode prevRoot = valRootMap.get(left.val);
int[] minMax = minMaxMap.get(prevRoot);
if (minMax[0] < legalRange[0] || minMax[1] > legalRange[1])
return null;
parent.left = prevRoot;
legalRangeMap.put(prevRoot, legalRange);
int[] parentMinMax = minMaxMap.get(parent);
int[] newMinMax = {minMax[0], parentMinMax[1]};
minMaxMap.put(prevRoot, newMinMax);
set.remove(prevRoot);
}
if (right != null && valRootMap.containsKey(right.val)) {
int[] legalRange = legalRangeMap.get(right);
TreeNode prevRoot = valRootMap.get(right.val);
int[] minMax = minMaxMap.get(prevRoot);
if (minMax[0] < legalRange[0] || minMax[1] > legalRange[1])
return null;
parent.right = prevRoot;
legalRangeMap.put(prevRoot, legalRange);
int[] parentMinMax = minMaxMap.get(parent);
int[] newMinMax = {parentMinMax[0], minMax[1]};
minMaxMap.put(prevRoot, newMinMax);
set.remove(prevRoot);
}
}
if (set.size() != 1)
return null;
List<TreeNode> remain = new ArrayList<TreeNode>(set);
TreeNode root = remain.get(0);
if (isValidBST(root))
return root;
return null;
}
public void getMinMax(Map<TreeNode, int[]> minMaxMap, TreeNode root) {
TreeNode minNode = root, maxNode = root;
while (minNode.left != null)
minNode = minNode.left;
while (maxNode.right != null)
maxNode = maxNode.right;
minMaxMap.put(root, new int[]{minNode.val, maxNode.val});
}
public void getLegalRange(Map<TreeNode, int[]> legalRangeMap, TreeNode node, int min, int max) {
if (node == null)
return;
legalRangeMap.put(node, new int[]{min, max});
getLegalRange(legalRangeMap, node.left, min, node.val - 1);
getLegalRange(legalRangeMap, node.right, node.val + 1, max);
}
public void visitLeaves(Map<Integer, Integer> leavesCountMap, TreeNode node, boolean isRoot) {
if (isLeaf(node)) {
if (!isRoot)
leavesCountMap.put(node.val, leavesCountMap.getOrDefault(node.val, 0) + 1);
} else {
if (node.left != null)
visitLeaves(leavesCountMap, node.left, false);
if (node.right != null)
visitLeaves(leavesCountMap, node.right, false);
}
}
public boolean isLeaf(TreeNode node) {
return node != null && node.left == null && node.right == null;
}
public TreeNode getLeafParent(TreeNode root) {
if (root.left != null && root.right != null)
return root;
if (root.left != null) {
if (isLeaf(root.left))
return root;
else
return root.left;
} else {
if (isLeaf(root.right))
return root;
else
return root.right;
}
}
public boolean isValidBST(TreeNode root) {
if (root == null)
return true;
TreeNode prev = null;
boolean flag = false;
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
while (node != null) {
stack.push(node);
node = node.left;
}
TreeNode curr = stack.pop();
if (prev != null) {
if (prev.val >= curr.val)
return false;
}
prev = curr;
node = curr.right;
}
return true;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).