2271. Maximum White Tiles Covered by a Carpet

Problem

You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.

You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere.

Return **the *maximum* number of white tiles that can be covered by the carpet**.

  Example 1:

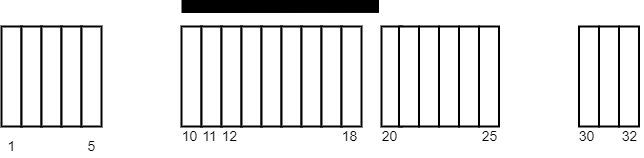
Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
Output: 9
Explanation: Place the carpet starting on tile 10. 
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.

Example 2:

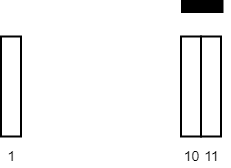
Input: tiles = [[10,11],[1,1]], carpetLen = 2
Output: 2
Explanation: Place the carpet starting on tile 10. 
It covers 2 white tiles, so we return 2.

  Constraints:

• 1 <= tiles.length <= 5 * 10^4

• tiles[i].length == 2

• 1 <= li <= ri <= 10^9

• 1 <= carpetLen <= 10^9

• The tiles are non-overlapping.

Solution (Java)

class Solution {
    public int maximumWhiteTiles(int[][] tiles, int carpetLength) {
        Arrays.sort(tiles, Comparator.comparingInt(x -> x[0]));
        int currentCover = Math.min(tiles[0][1] - tiles[0][0] + 1, carpetLength);
        int maxCover = currentCover;
        int head = 1;
        int tail = 0;
        while (tail < tiles.length && head < tiles.length && maxCover < carpetLength) {
            if (tiles[head][1] - tiles[tail][0] + 1 <= carpetLength) {
                currentCover += tiles[head][1] - tiles[head][0] + 1;
                maxCover = Math.max(maxCover, currentCover);
                ++head;
            } else {
                int possiblePartialCoverOverCurrentHead =
                        carpetLength - (tiles[head][0] - tiles[tail][0]);
                maxCover = Math.max(maxCover, currentCover + possiblePartialCoverOverCurrentHead);
                currentCover = currentCover - (tiles[tail][1] - tiles[tail][0] + 1);
                ++tail;
            }
        }
        return maxCover;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).