2218. Maximum Value of K Coins From Piles

Problem

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return **the *maximum total value* of coins you can have in your wallet if you choose exactly** k coins optimally.

  Example 1:

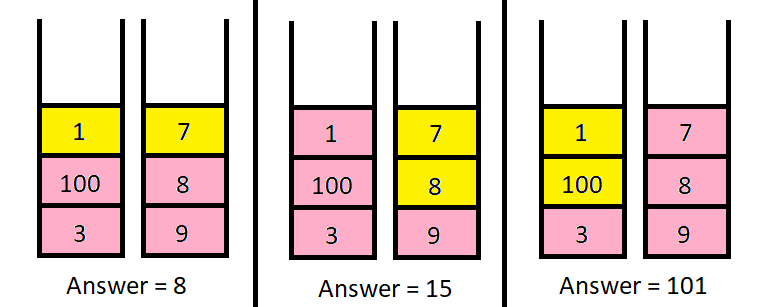
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

  Constraints:

• n == piles.length

• 1 <= n <= 1000

• 1 <= piles[i][j] <= 10^5

• 1 <= k <= sum(piles[i].length) <= 2000

Solution

class Solution {
    public int maxValueOfCoins(List<List<Integer>> piles, int k) {
        int[] dp = new int[k + 1];
        for (List<Integer> pile : piles) {
            int m = pile.size();
            int[] cum = new int[m + 1];
            for (int i = 0; i < m; i++) {
                cum[i + 1] = cum[i] + pile.get(i);
            }
            int[] curdp = new int[k + 1];
            for (int i = 0; i <= k; i++) {
                for (int j = 0; j <= m && i + j <= k; j++) {
                    curdp[i + j] = Math.max(curdp[i + j], dp[i] + cum[j]);
                }
            }
            dp = curdp;
        }
        return dp[k];
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).