2503. Maximum Number of Points From Grid Queries

Problem

You are given an m x n integer matrix grid and an array queries of size k.

Find an array answer of size k such that for each integer queres[i] you start in the top left cell of the matrix and repeat the following process:

• If queries[i] is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all 4 directions: up, down, left, and right.

• Otherwise, you do not get any points, and you end this process.

After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times.

Return the resulting array answer.

  Example 1:

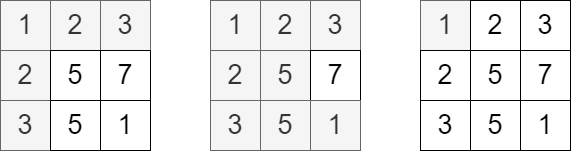
Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
Output: [5,8,1]
Explanation: The diagrams above show which cells we visit to get points for each query.

Example 2:

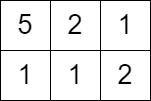
Input: grid = [[5,2,1],[1,1,2]], queries = [3]
Output: [0]
Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3.

  Constraints:

• m == grid.length

• n == grid[i].length

• 2 <= m, n <= 1000

• 4 <= m * n <= 105

• k == queries.length

• 1 <= k <= 104

• 1 <= grid[i][j], queries[i] <= 106

Solution (Java)

class Solution {
    private static final int[][] DIRS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public int[] maxPoints(int[][] grid, int[] queries) {
        int m = grid.length;
        int n = grid[0].length;
        boolean[][] visited = new boolean[m][n];

        // map will store the number of points possible: query -> points
        TreeMap<Integer, Integer> pointsMap = new TreeMap<>();

        // use heap to visit reachable nodes in increasing order of cell value
        PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[2] - b[2]);
        heap.offer(new int[] { 0, 0, grid[0][0] });  // row, col, cell value
        visited[0][0] = true;
        int points = 0;

        while (!heap.isEmpty()) {
            // the smallest query value needed to get to the next unvisited node,
            // we add 1 because queries[i] must be strictly greater than cell value
            int query = heap.peek()[2] + 1;

            // BFS - visit all nodes with cell value strictly less than query
            while (!heap.isEmpty() && heap.peek()[2] < query) {
                int[] entry = heap.poll();
                int row = entry[0];
                int col = entry[1];
                points++;

                for (int[] dir : DIRS) {
                    int r = row + dir[0];
                    int c = col + dir[1];
                    if (r >= 0 && r < m && c >= 0 && c < n && !visited[r][c]) {
                        heap.offer(new int[] { r, c, grid[r][c] });
                        visited[r][c] = true;
                    }
                }
            }

            // store points for query value
            pointsMap.put(query, points);
        }

        // handle each query
        int[] output = new int[queries.length];
        for (int i = 0; i < queries.length; i++) {
            // use floorKey to key with maximum number of points for this query
            Integer key = pointsMap.floorKey(queries[i]);
            if (key != null) {
                output[i] = pointsMap.get(key);
            } else {
                output[i] = 0;
            }
        }
        return output;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).