1453. Maximum Number of Darts Inside of a Circular Dartboard

Problem

Alice is throwing n darts on a very large wall. You are given an array darts where darts[i] = [xi, yi] is the position of the ith dart that Alice threw on the wall.

Bob knows the positions of the n darts on the wall. He wants to place a dartboard of radius r on the wall so that the maximum number of darts that Alice throws lies on the dartboard.

Given the integer r, return the maximum number of darts that can lie on the dartboard.

  Example 1:

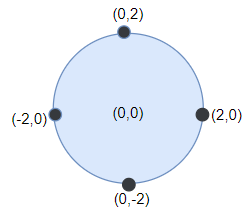
Input: darts = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
Output: 4
Explanation: Circle dartboard with center in (0,0) and radius = 2 contain all points.

Example 2:

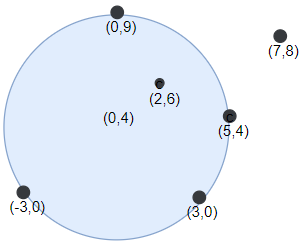
Input: darts = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
Output: 5
Explanation: Circle dartboard with center in (0,4) and radius = 5 contain all points except the point (7,8).

  Constraints:

• 1 <= darts.length <= 100

• darts[i].length == 2

• -10^4 <= xi, yi <= 10^4

• 1 <= r <= 5000

Solution

class Solution {
    private static class Angle implements Comparable<Angle> {
        double a;
        boolean enter;

        Angle(double a, boolean enter) {
            this.a = a;
            this.enter = enter;
        }

        @Override
        public int compareTo(Angle o) {
            if (a > o.a) {
                return 1;
            } else if (a < o.a) {
                return -1;
            } else if (enter == o.enter) {
                return 0;
            } else if (enter) {
                return -1;
            }
            return 1;
        }
    }

    private int getPointsInside(int i, double r, int n, int[][] points, double[][] dis) {
        List<Angle> angles = new ArrayList<>(2 * n);
        for (int j = 0; j < n; j++) {
            if (i != j && dis[i][j] <= 2 * r) {
                double b = Math.acos(dis[i][j] / (2 * r));
                double a =
                        Math.atan2(
                                points[j][1] - points[i][1] * 1.0,
                                points[j][0] * 1.0 - points[i][0]);
                double alpha = a - b;
                double beta = a + b;
                angles.add(new Angle(alpha, true));
                angles.add(new Angle(beta, false));
            }
        }
        Collections.sort(angles);
        int count = 1;
        int res = 1;
        for (Angle a : angles) {
            if (a.enter) {
                count++;
            } else {
                count--;
            }
            if (count > res) {
                res = count;
            }
        }
        return res;
    }

    public int numPoints(int[][] points, int r) {
        int n = points.length;
        double[][] dis = new double[n][n];
        for (int i = 0; i < n - 1; i++) {
            for (int j = i + 1; j < n; j++) {
                dis[i][j] =
                        dis[j][i] =
                                Math.sqrt(
                                        Math.pow(points[i][0] * 1.0 - points[j][0], 2)
                                                + Math.pow(points[i][1] * 1.0 - points[j][1], 2));
            }
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans = Math.max(ans, getPointsInside(i, r, n, points, dis));
        }
        return ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).