1840. Maximum Building Height

Problem

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

• The height of each building must be a non-negative integer.

• The height of the first building must be 0.

• The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return **the *maximum possible height* of the tallest building**.

  Example 1:

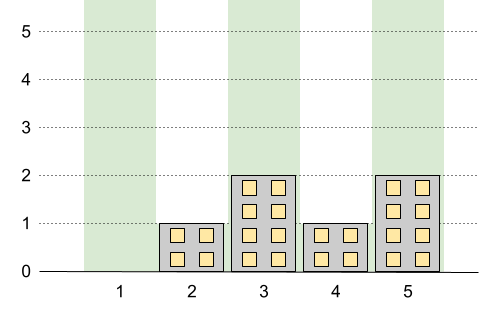
Input: n = 5, restrictions = [[2,1],[4,1]]
Output: 2
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

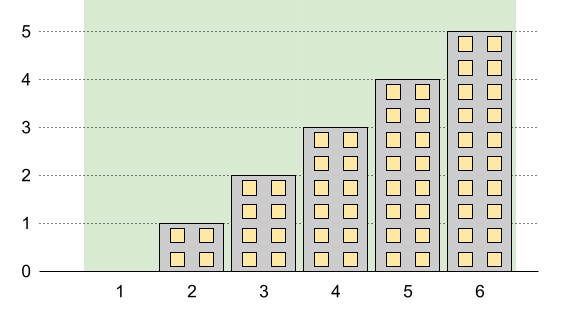
Input: n = 6, restrictions = []
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

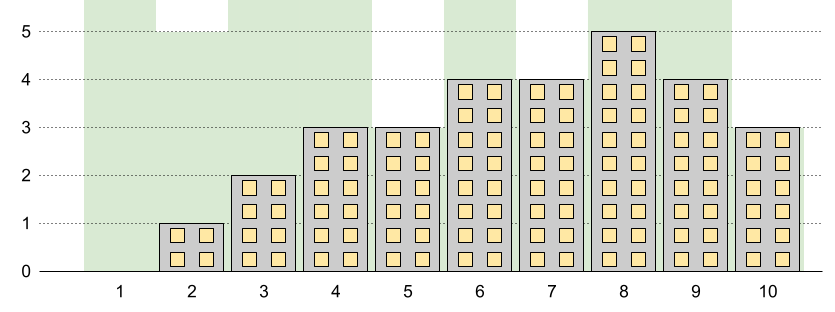
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

  Constraints:

• 2 <= n <= 10^9

• 0 <= restrictions.length <= min(n - 1, 10^5)

• 2 <= idi <= n

• idi is unique.

• 0 <= maxHeighti <= 10^9

Solution

class Solution {
    public int maxBuilding(int n, int[][] restrictions) {
        if (restrictions.length == 0) {
            return n - 1;
        }
        int m = restrictions.length;
        Arrays.sort(restrictions, Comparator.comparingInt(a -> a[0]));
        for (int i = m - 2; i >= 0; i--) {
            restrictions[i][1] =
                    Math.min(
                            restrictions[i][1],
                            restrictions[i + 1][1] + restrictions[i + 1][0] - restrictions[i][0]);
        }
        int id = 1;
        int height = 0;
        int res = 0;
        for (int[] r : restrictions) {
            int currMax;
            if (r[1] >= height + r[0] - id) {
                currMax = height + r[0] - id;
                height = currMax;
            } else {
                currMax = (height + r[0] - id + r[1]) / 2;
                height = r[1];
            }
            id = r[0];
            res = Math.max(res, currMax);
        }
        if (id != n) {
            res = Math.max(res, height + n - id);
        }
        return res;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).