1615. Maximal Network Rank

Problem

There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [ai, bi] indicates that there is a bidirectional road between cities ai and bi.

The network rank** **of *two different cities* is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.

The **maximal network rank **of the infrastructure is the maximum network rank of all pairs of different cities.

Given the integer n and the array roads, return **the *maximal network rank* of the entire infrastructure**.

  Example 1:

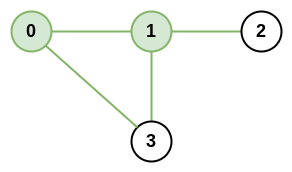
Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.

Example 2:

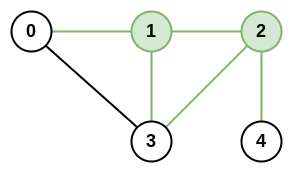
Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
Output: 5
Explanation: There are 5 roads that are connected to cities 1 or 2.

Example 3:

Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
Output: 5
Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.

  Constraints:

• 2 <= n <= 100

• 0 <= roads.length <= n * (n - 1) / 2

• roads[i].length == 2

• 0 <= ai, bi&nbsp;<= n-1

• ai != bi

• Each pair of cities has at most one road connecting them.

Solution (Java)

class Solution {
    public int maximalNetworkRank(int n, int[][] roads) {
        int[] degrees = new int[n];
        boolean[] connected = new boolean[40_000];
        for (int[] r : roads) {
            degrees[r[0]]++;
            degrees[r[1]]++;
            connected[(r[0] + 101) * (r[1] + 101) - 1] = true;
        }
        int max = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (connected[(i + 101) * (j + 101) - 1]) {
                    max = Math.max(max, degrees[i] + degrees[j] - 1);
                } else {
                    max = Math.max(max, degrees[i] + degrees[j]);
                }
            }
        }
        return max;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).