2673. Make Costs of Paths Equal in a Binary Tree

Problem

You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left child is the node 2 * i and the right child is 2 * i + 1.

Each node in the tree also has a cost represented by a given 0-indexed integer array cost of size n where cost[i] is the cost of node i + 1. You are allowed to increment the cost of any node by 1 any number of times.

Return **the *minimum* number of increments you need to make the cost of paths from the root to each leaf node equal**.

Note:

• A **perfect binary tree **is a tree where each node, except the leaf nodes, has exactly 2 children.
• The cost of a path is the sum of costs of nodes in the path.

Example 1:

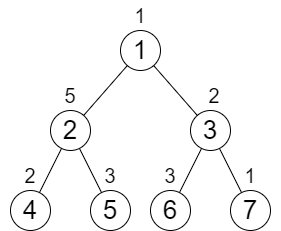
Input: n = 7, cost = [1,5,2,2,3,3,1]
Output: 6
Explanation: We can do the following increments:
- Increase the cost of node 4 one time.
- Increase the cost of node 3 three times.
- Increase the cost of node 7 two times.
Each path from the root to a leaf will have a total cost of 9.
The total increments we did is 1 + 3 + 2 = 6.
It can be shown that this is the minimum answer we can achieve.

Example 2:

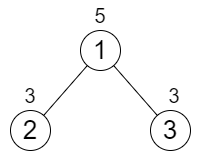
Input: n = 3, cost = [5,3,3]
Output: 0
Explanation: The two paths already have equal total costs, so no increments are needed.

Constraints:

• 3 <= n <= 105
• n + 1 is a power of 2
• cost.length == n
• 1 <= cost[i] <= 104

Solution (Java)

class Solution {
    int res = 0;
    public int minIncrements(int n, int[] cost) {
        dfs(0, cost);
        return res;
    }
    private int dfs(int i, int[] cost) {
        if (i >= cost.length) return 0;
        int a = dfs(2 * i + 1, cost), b = dfs(2 * i + 2, cost);
        res += Math.abs(a - b);
        return cost[i] + Math.max(a, b);
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).