Problem
Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.
Recall that:
The node of a binary tree is a leaf if and only if it has no children
The depth of the root of the tree is
0. if the depth of a node isd, the depth of each of its children isd + 1.The lowest common ancestor of a set
Sof nodes, is the nodeAwith the largest depth such that every node inSis in the subtree with rootA.
Example 1:
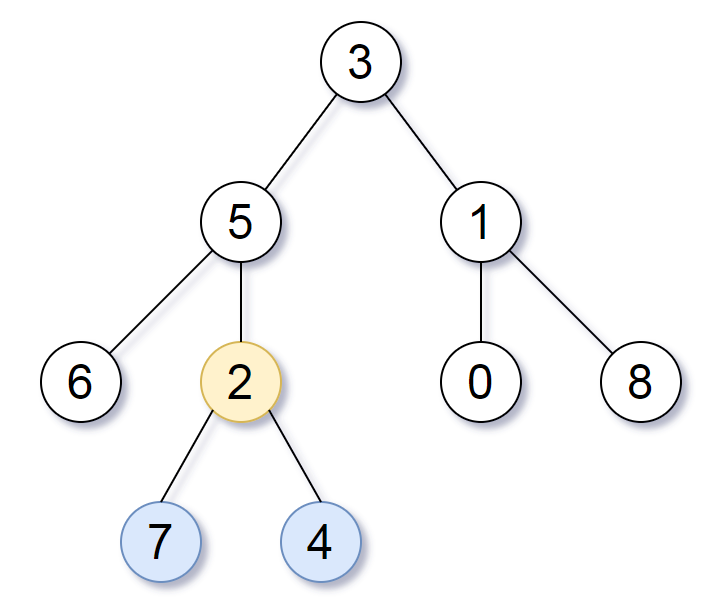
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest leaf-nodes of the tree.
Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.
Example 2:
Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree, and it's the lca of itself.
Example 3:
Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.
Constraints:
The number of nodes in the tree will be in the range
[1, 1000].0 <= Node.val <= 1000The values of the nodes in the tree are unique.
Note: This question is the same as 865: https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode lcaDeepestLeaves(TreeNode root) {
if (root == null) {
return null;
}
int leftDep = getDep(root.left);
int rightDep = getDep(root.right);
if (leftDep == rightDep) {
return root;
} else {
if (leftDep > rightDep) {
return lcaDeepestLeaves(root.left);
} else {
return lcaDeepestLeaves(root.right);
}
}
}
public int getDep(TreeNode root) {
if (root == null) {
return 0;
}
return 1 + Math.max(getDep(root.left), getDep(root.right));
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).