Problem
You are given the root of a binary tree.
A ZigZag path for a binary tree is defined as follow:
Choose **any **node in the binary tree and a direction (right or left).
If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
Change the direction from right to left or from left to right.
Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return **the longest *ZigZag* path contained in that tree**.
Example 1:
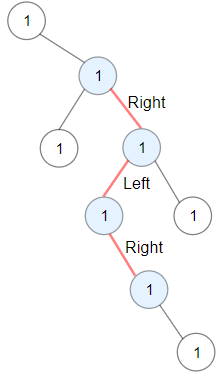
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).
Example 2:
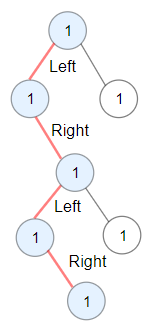
Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).
Example 3:
Input: root = [1]
Output: 0
Constraints:
The number of nodes in the tree is in the range
[1, 5 * 10^4].1 <= Node.val <= 100
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int maxLength = 0;
public int longestZigZag(TreeNode root) {
dfs(root, true);
return maxLength;
}
private int dfs(TreeNode root, boolean isLeft) {
if (root == null) {
return 0;
}
int left = dfs(root.left, false);
int right = dfs(root.right, true);
maxLength = Math.max(maxLength, left);
maxLength = Math.max(maxLength, right);
return 1 + (isLeft ? left : right);
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).