Problem
Given an array of points on the X-Y plane points where points[i] = [xi, yi], return the area of the largest triangle that can be formed by any three different points. Answers within 10-5 of the actual answer will be accepted.
Example 1:
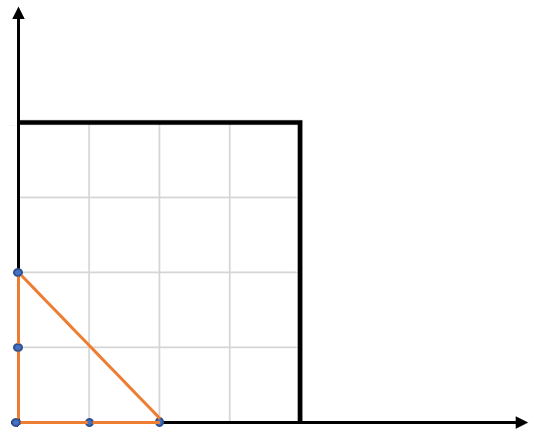
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2.00000
Explanation: The five points are shown in the above figure. The red triangle is the largest.
Example 2:
Input: points = [[1,0],[0,0],[0,1]]
Output: 0.50000
Constraints:
3 <= points.length <= 50-50 <= xi, yi <= 50All the given points are unique.
Solution (Java)
class Solution {
public double largestTriangleArea(int[][] points) {
int n = points.length;
double max = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
for (int k = j + 1; k < n; k++) {
double area;
int[] a = points[i];
int[] b = points[j];
int[] c = points[k];
area = Math.abs(area(a, b) + area(b, c) + area(c, a));
if (area > max) {
max = area;
}
}
}
}
return max;
}
private double area(int[] a, int[] b) {
int l = b[0] - a[0];
double h = (a[1] + b[1] + 200) / 2.0;
return l * h;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).