764. Largest Plus Sign

Problem

You are given an integer n. You have an n x n binary grid grid with all values initially 1's except for some indices given in the array mines. The ith element of the array mines is defined as mines[i] = [xi, yi] where grid[xi][yi] == 0.

Return **the order of the largest *axis-aligned* plus sign of 1's contained in **grid. If there is none, return 0.

An axis-aligned plus sign of 1's of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1's. Note that there could be 0's or 1's beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1's.

  Example 1:

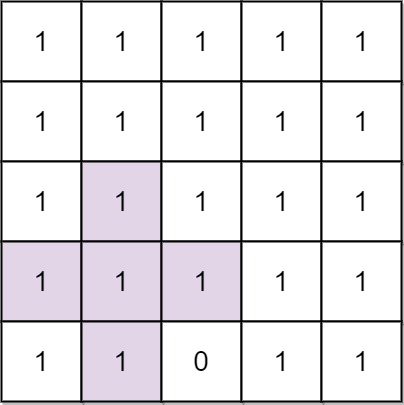
Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.

Example 2:

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.

  Constraints:

• 1 <= n <= 500

• 1 <= mines.length <= 5000

• 0 <= xi, yi < n

• All the pairs (xi, yi) are unique.

Solution (Java)

class Solution {
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        boolean[][] mat = new boolean[n][n];
        for (int[] pos : mines) {
            mat[pos[0]][pos[1]] = true;
        }
        int[][] left = new int[n][n];
        int[][] right = new int[n][n];
        int[][] up = new int[n][n];
        int[][] down = new int[n][n];
        int ans = 0;
        // For Left and Up only
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                int i1 = j == 0 ? 0 : left[i][j - 1];
                left[i][j] = mat[i][j] ? 0 : 1 + i1;
                int i2 = i == 0 ? 0 : up[i - 1][j];
                up[i][j] = mat[i][j] ? 0 : 1 + i2;
            }
        }
        // For Right and Down and simoultaneously get answer
        for (int i = n - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                int i1 = j == n - 1 ? 0 : right[i][j + 1];
                right[i][j] = mat[i][j] ? 0 : 1 + i1;
                int i2 = i == n - 1 ? 0 : down[i + 1][j];
                down[i][j] = mat[i][j] ? 0 : 1 + i2;
                int x = Math.min(Math.min(left[i][j], up[i][j]), Math.min(right[i][j], down[i][j]));
                ans = Math.max(ans, x);
            }
        }
        return ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).