668. Kth Smallest Number in Multiplication Table

Problem

Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).

Given three integers m, n, and k, return **the *kth* smallest element in the m x n multiplication table**.

  Example 1:

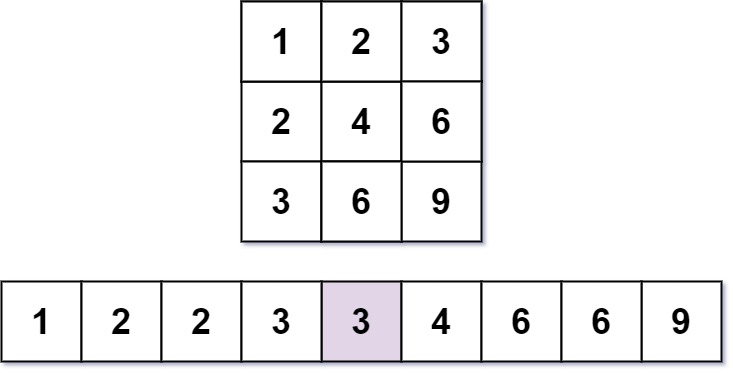
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.

Example 2:

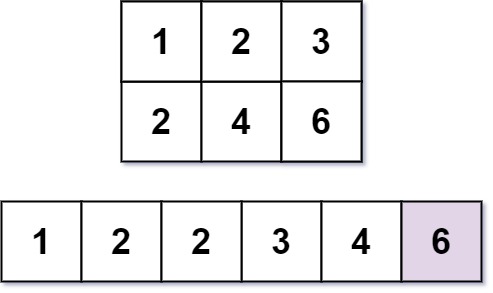
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.

  Constraints:

• 1 <= m, n <= 3 * 10^4

• 1 <= k <= m * n

Solution

/**
 * @param {number} m
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var findKthNumber = function(m, n, k) {
    // Check how many numbers per row x is greater than
    function enough(x) {
        let count = 0;
        for (let i = 1; i <= m; i++) {
            count += Math.min(Math.floor(x / i), n);
        }
        return count >= k;
    }

    let lo = 1, hi = m * n;
    // Binary search template
    while (lo < hi) {
        let mi = lo + Math.floor((hi - lo) / 2);
        if (enough(mi)) hi = mi;
        else lo = mi + 1;
    }
    return lo;
};

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).