2583. Kth Largest Sum in a Binary Tree

Problem

You are given the root of a binary tree and a positive integer k.

The level sum in the tree is the sum of the values of the nodes that are on the same level.

Return** the **kth** *largest* level sum in the tree (not necessarily distinct)**. If there are fewer than k levels in the tree, return -1.

Note that two nodes are on the same level if they have the same distance from the root.

Example 1:

Input: root = [5,8,9,2,1,3,7,4,6], k = 2
Output: 13
Explanation: The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.

Example 2:

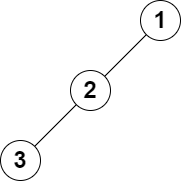
Input: root = [1,2,null,3], k = 1
Output: 3
Explanation: The largest level sum is 3.

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= 106
• 1 <= k <= n

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public long kthLargestLevelSum(TreeNode root, int k) {
        Queue<TreeNode>q=new LinkedList<>();
        q.add(root);
        //long maxSum=0;

        ArrayList<Long>maxArray=new ArrayList<>();
        while(!q.isEmpty()){

            List<Integer>list=new ArrayList<>();
            int count=q.size();

            for(int i=0;i<count;i++){
                TreeNode cur=q.poll();
                list.add(cur.val);
                if(cur.left!=null){
                    q.add(cur.left);
                }
                if(cur.right!=null){
                    q.add(cur.right);
                }
            }

            long sum=0;
            for(int i=0;i<list.size();i++){
                sum+=list.get(i);
            }
            maxArray.add(sum);


        }
        if(k>maxArray.size()) return -1;
        Collections.sort(maxArray);
        return maxArray.get(maxArray.size()-k);
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).