Graph Connectivity With Threshold

Problem

We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

x % z == 0,
y % z == 0, and
z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [ai, bi] if cities ai and bi are connected directly or indirectly. (i.e. there is some path between them).

Return **an array *answer*, where *answer.length == queries.length* and answer[i] is true if for the ith query, there is a path between ai and bi, or answer[i] is false if there is no path.**

Example 1:

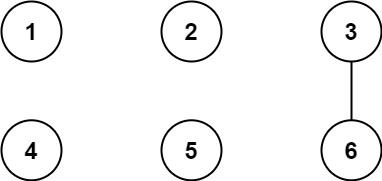
Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
Output: [false,false,true]
Explanation: The divisors for each number:
1:   1
2:   1, 2
3:   1, 3
4:   1, 2, 4
5:   1, 5
6:   1, 2, 3, 6
Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the
only ones directly connected. The result of each query:
[1,4]   1 is not connected to 4
[2,5]   2 is not connected to 5
[3,6]   3 is connected to 6 through path 3--6

Example 2:

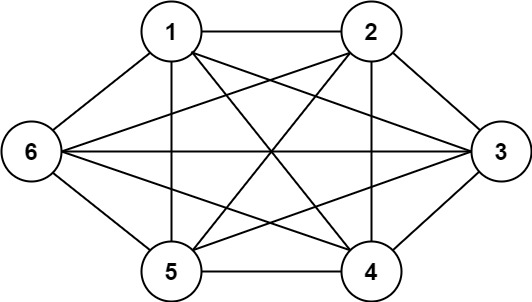
Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
Output: [true,true,true,true,true]
Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0,
all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.

Example 3:

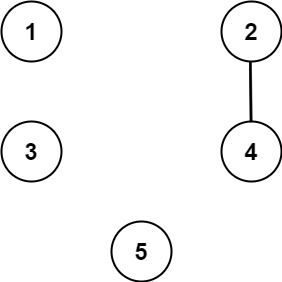
Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
Output: [false,false,false,false,false]
Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected.
Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].

Constraints:

2 <= n <= 10^4
0 <= threshold <= n
1 <= queries.length <= 10^5
queries[i].length == 2
1 <= ai, bi <= cities
ai != bi

Solution

class Solution {
    public List<Boolean> areConnected(int n, int threshold, int[][] queries) {
        if (n < 1 || queries == null || queries.length == 0) {
            return new ArrayList<>();
        }
        int i;
        int j;
        int k;
        int x;
        DisjointSetUnion set = new DisjointSetUnion(n + 1);
        int edges = queries.length;
        for (i = threshold + 1; i <= n; i++) {
            k = n / i;
            x = i;
            for (j = 2; j <= k; j++) {
                x = x + i;
                set.union(i, x);
            }
        }
        List<Boolean> result = new ArrayList<>(edges);
        for (int[] query : queries) {
            result.add(set.find(query[0]) == set.find(query[1]));
        }
        return result;
    }

    private static class DisjointSetUnion {
        private final int[] rank;
        private final int[] parent;

        public DisjointSetUnion(int n) {
            rank = new int[n];
            parent = new int[n];
            for (int i = 0; i < n; i++) {
                this.rank[i] = 1;
                this.parent[i] = i;
            }
        }

        public int find(int u) {
            int x = u;
            while (x != parent[x]) {
                x = parent[x];
            }
            parent[u] = x;
            return x;
        }

        public void union(int u, int v) {
            if (u != v) {
                int x = find(u);
                int y = find(v);
                if (x != y) {
                    if (rank[x] > rank[y]) {
                        rank[x] += rank[y];
                        parent[y] = x;
                    } else {
                        rank[y] += rank[x];
                        parent[x] = y;
                    }
                }
            }
        }
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).