Problem
For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.
Example 1:
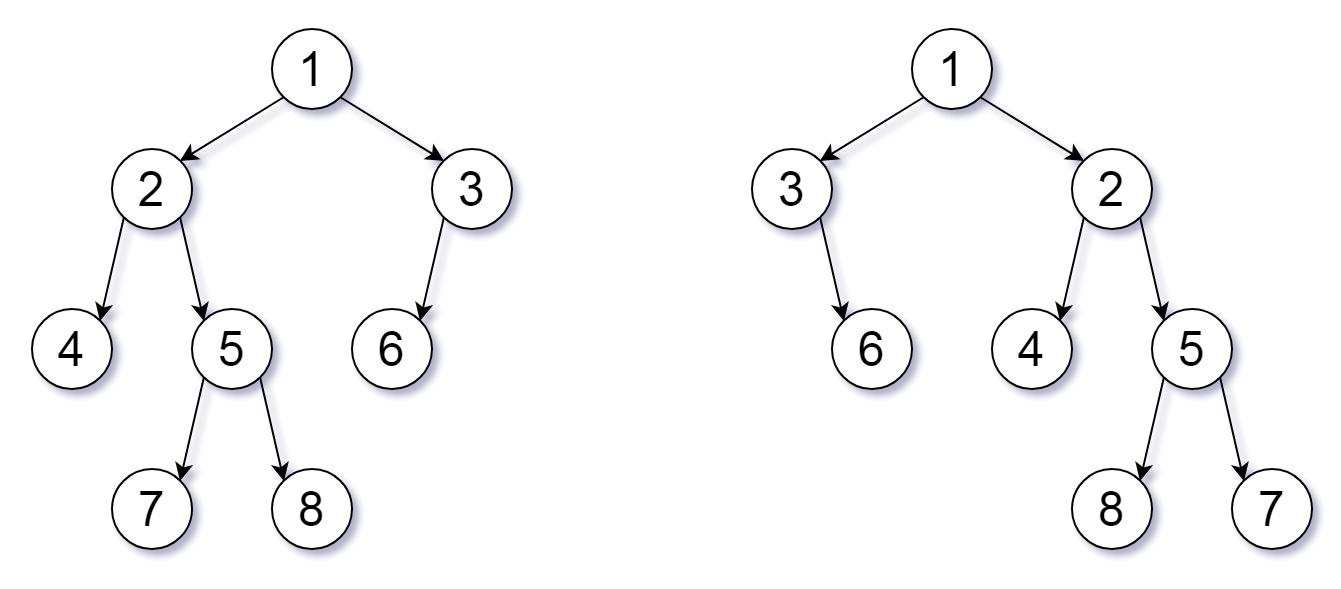
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.
Example 2:
Input: root1 = [], root2 = []
Output: true
Example 3:
Input: root1 = [], root2 = [1]
Output: false
Constraints:
The number of nodes in each tree is in the range
[0, 100].Each tree will have unique node values in the range
[0, 99].
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null) {
return true;
}
if (root1 == null || root2 == null) {
return false;
}
if (root1.val != root2.val) {
return false;
}
return flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right)
|| flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left);
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).