979. Distribute Coins in Binary Tree

Problem

You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return **the *minimum* number of moves required to make every node have exactly one coin**.

  Example 1:

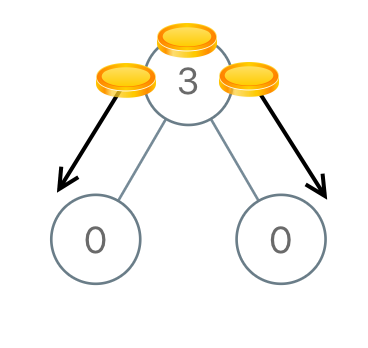
Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

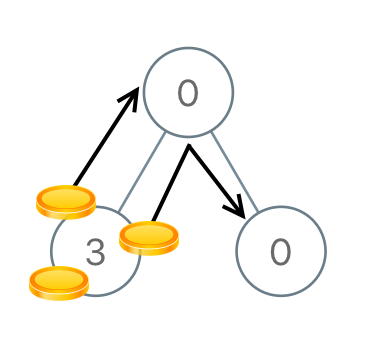
Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

  Constraints:

• The number of nodes in the tree is n.

• 1 <= n <= 100

• 0 <= Node.val <= n

• The sum of all Node.val is n.

Solution (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int num = 0;

    public int distributeCoins(TreeNode root) {
        helper(root);
        return num;
    }

    private int helper(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int total = node.val + helper(node.left) + helper(node.right);
        int leftover = total - 1;
        num += Math.abs(leftover);
        return leftover;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).