2509. Cycle Length Queries in a Tree

Problem

You are given an integer n. There is a complete binary tree with 2n - 1 nodes. The root of that tree is the node with the value 1, and every node with a value val in the range [1, 2n - 1 - 1] has two children where:

• The left node has the value 2 * val, and

• The right node has the value 2 * val + 1.

You are also given a 2D integer array queries of length m, where queries[i] = [ai, bi]. For each query, solve the following problem:

• Add an edge between the nodes with values ai and bi.

• Find the length of the cycle in the graph.

• Remove the added edge between nodes with values ai and bi.

Note that:

• A cycle is a path that starts and ends at the same node, and each edge in the path is visited only once.

• The length of a cycle is the number of edges visited in the cycle.

• There could be multiple edges between two nodes in the tree after adding the edge of the query.

Return **an array *answer* of length m where** answer[i] is the answer to the ith query.

  Example 1:

Input: n = 3, queries = [[5,3],[4,7],[2,3]]
Output: [4,5,3]
Explanation: The diagrams above show the tree of 23 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 3 and 5, the graph contains a cycle of nodes [5,2,1,3]. Thus answer to the first query is 4. We delete the added edge and process the next query.
- After adding the edge between nodes 4 and 7, the graph contains a cycle of nodes [4,2,1,3,7]. Thus answer to the second query is 5. We delete the added edge and process the next query.
- After adding the edge between nodes 2 and 3, the graph contains a cycle of nodes [2,1,3]. Thus answer to the third query is 3. We delete the added edge.

Example 2:

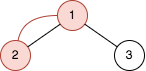
Input: n = 2, queries = [[1,2]]
Output: [2]
Explanation: The diagram above shows the tree of 22 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 1 and 2, the graph contains a cycle of nodes [2,1]. Thus answer for the first query is 2. We delete the added edge.

  Constraints:

• 2 <= n <= 30

• m == queries.length

• 1 <= m <= 105

• queries[i].length == 2

• 1 <= ai, bi <= 2n - 1

• ai != bi

Solution (Java)

class Solution {
    public int[] cycleLengthQueries(int n, int[][] queries) {
        var res = new int[queries.length];

        for (int i = 0; i < res.length; i++) {
            var a = getRootPath(queries[i][0]);
            var b = getRootPath(queries[i][1]);
            while (a.size() > 0 && b.size() > 0 && a.get(a.size() - 1).equals(b.get(b.size() - 1))) {
                a.remove(a.size() - 1);
                b.remove(b.size() - 1);
            }
            res[i] = a.size() + b.size() + 1;
        }

        return res;
    }

    private List<Integer> getRootPath(int u) {
        var path = new ArrayList<Integer>();
        while (u != 0) {
            path.add(u);
            u /= 2;
        }
        return path;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).