Problem
Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Return **the *root* of the modified tree**.
Note that the depth of a node is the number of edges in the path from the root node to it.
Example 1:
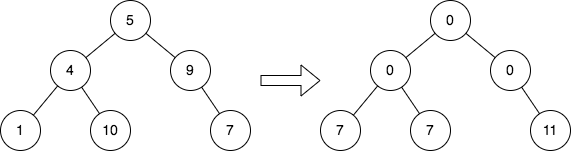
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.
Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 104
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode replaceValueInTree(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
Map<TreeNode, List<Integer>> map = new HashMap<>();
root.val = 0;
while(!q.isEmpty()) {
int size = q.size();
int sum = 0;
map = new HashMap<>();
for(int i = 0; i < size; i++) {
TreeNode cur = q.poll();
map.put(cur, new ArrayList<>());
if(cur.left != null) {
sum += cur.left.val;
q.add(cur.left);
map.get(cur).add(cur.left.val);
}
if(cur.right != null) {
sum += cur.right.val;
q.add(cur.right);
map.get(cur).add(cur.right.val);
}
}
for(Map.Entry<TreeNode,List<Integer>> entry : map.entrySet()) {
if(entry.getValue().size() == 2) {
int num = entry.getValue().get(0)+entry.getValue().get(1);
entry.getKey().left.val = sum - num;
entry.getKey().right.val = sum - num;
} else if(entry.getValue().size() == 1) {
if(entry.getKey().left != null) entry.getKey().left.val = sum - entry.getValue().get(0);
else if(entry.getKey().right != null) entry.getKey().right.val = sum - entry.getValue().get(0);
}
}
}
return root;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).