2316. Count Unreachable Pairs of Nodes in an Undirected Graph

Problem

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return **the *number of pairs* of different nodes that are unreachable from each other**.

  Example 1:

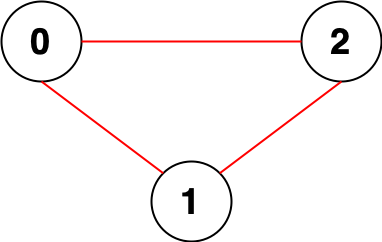
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

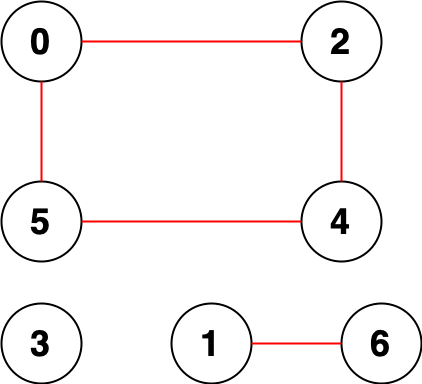
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

  Constraints:

• 1 <= n <= 10^5

• 0 <= edges.length <= 2 * 10^5

• edges[i].length == 2

• 0 <= ai, bi < n

• ai != bi

• There are no repeated edges.

Solution (Java)

class Solution {
    public long countPairs(int n, int[][] edges) {
        DSU d = new DSU(n);
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int[] e : edges) {
            d.union(e[0], e[1]);
        }
        long ans = 0;
        for (int i = 0; i < n; i++) {
            int p = d.findParent(i);
            int cnt = map.containsKey(p) ? map.get(p) : 0;
            ans += i - cnt;
            map.put(p, map.getOrDefault(p, 0) + 1);
        }
        return ans;
    }

    private static class DSU {
        int[] rank;
        int[] parent;

        DSU(int n) {
            rank = new int[n + 1];
            parent = new int[n + 1];
            for (int i = 1; i <= n; i++) {
                parent[i] = i;
            }
        }

        int findParent(int node) {
            if (parent[node] == node) {
                return node;
            }
            parent[node] = findParent(parent[node]);
            return findParent(parent[node]);
        }

        boolean union(int x, int y) {
            int px = findParent(x);
            int py = findParent(y);
            if (px == py) {
                return false;
            }
            if (rank[px] > rank[py]) {
                parent[py] = px;
            } else {
                parent[px] = py;
                rank[py]++;
            }
            return true;
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).