2791. Count Paths That Can Form a Palindrome in a Tree

Problem

You are given a tree (i.e. a connected, undirected graph that has no cycles) rooted at node 0 consisting of n nodes numbered from 0 to n - 1. The tree is represented by a 0-indexed array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to the edge between i and parent[i]. s[0] can be ignored.

Return **the number of pairs of nodes *(u, v)* such that u < v and the characters assigned to edges on the path from u to v can be rearranged to form a **palindrome****.

A string is a palindrome when it reads the same backwards as forwards.

Example 1:

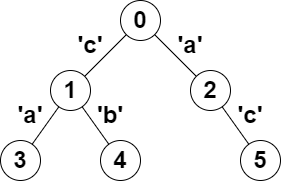
Input: parent = [-1,0,0,1,1,2], s = "acaabc"
Output: 8
Explanation: The valid pairs are:
- All the pairs (0,1), (0,2), (1,3), (1,4) and (2,5) result in one character which is always a palindrome.
- The pair (2,3) result in the string "aca" which is a palindrome.
- The pair (1,5) result in the string "cac" which is a palindrome.
- The pair (3,5) result in the string "acac" which can be rearranged into the palindrome "acca".

Example 2:

Input: parent = [-1,0,0,0,0], s = "aaaaa"
Output: 10
Explanation: Any pair of nodes (u,v) where u < v is valid.

Constraints:

• n == parent.length == s.length
• 1 <= n <= 105
• 0 <= parent[i] <= n - 1 for all i >= 1
• parent[0] == -1
• parent represents a valid tree.
• s consists of only lowercase English letters.

Solution (Java)

class Solution {

    List<int []> [] graph;

    int [] nodeVals;

    Map<Integer, Integer> map;

    public long countPalindromePaths(List<Integer> parent, String s) {
        int n = parent.size();

        graph = new List[n];

        for (int i = 0; i < n; ++i) {
            graph[i] = new ArrayList<>();
        }

        for (int i = 1; i < n; ++i) {
            // node, bitMaskVal
            graph[parent.get(i)].add(new int [] {i, s.charAt(i) - 'a'});
        }

        nodeVals = new int [n];

        map = new HashMap<>();

        dfs(0, 0);

        long total = 0;
        long val;
        int current, nCurrent;

        for (int i = 0; i < n; ++i) {
            current = nodeVals[i];

            val = map.get(current) - 1;

            for (int j = 0; j <= 26; ++j) {
                nCurrent = current ^ (1 << j);
                val += map.getOrDefault(nCurrent, 0);
            }

            total += val;
        }

        return total / 2;
    }

    private void dfs(int node, int val) {
        nodeVals[node] = val;
        int nextNode, nextBit;

        map.put(val, map.getOrDefault(val, 0) + 1);

        for (int [] next : graph[node]) {
            nextNode = next[0];
            nextBit = next[1];

            dfs(nextNode, val ^ (1 << nextBit));
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).