Problem
There is a street with n * 2 plots, where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.
Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 10^9 + 7.
Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.
Example 1:
Input: n = 1
Output: 4
Explanation:
Possible arrangements:
1. All plots are empty.
2. A house is placed on one side of the street.
3. A house is placed on the other side of the street.
4. Two houses are placed, one on each side of the street.
Example 2:
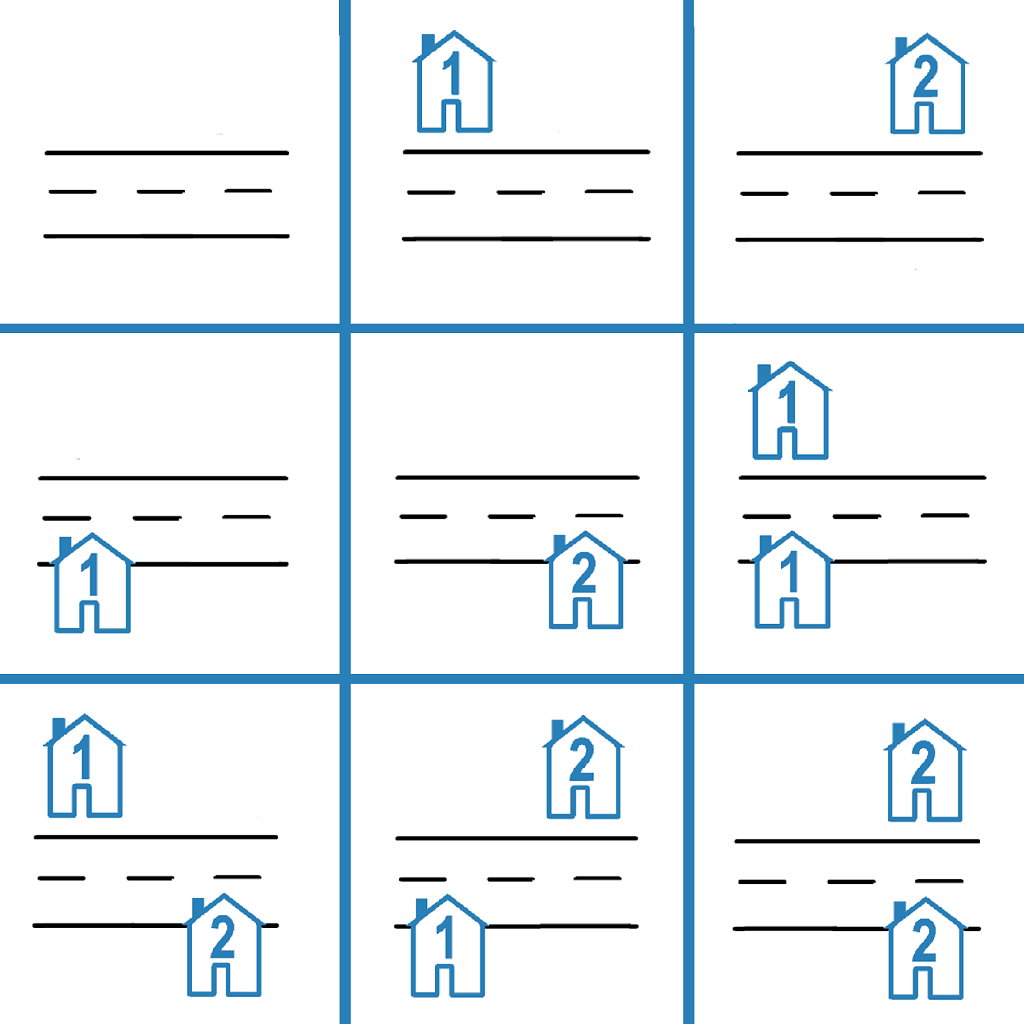
Input: n = 2
Output: 9
Explanation: The 9 possible arrangements are shown in the diagram above.
Constraints:
1 <= n <= 10^4
Solution (Java)
class Solution {
public int countHousePlacements(int n) {
// algo - 1st solve one side of the street
// think 0 - space , 1 - house
// if n = 1 then we can take one 0 and one 1 (total ways = 2)
// if n = 2 then 00 , 01 , 10 , 11 but we cant take 11 as two house cant be adjacent.
// so the 1 ended string will be only 1 which is same as previous 0 ended string and 0 ended
// string are 2 which is previous sum(total ways)
// apply this formula for n no's
long mod = 1000000007;
long space = 1;
long house = 1;
long sum = space + house;
while (--n > 0) {
house = space;
space = sum;
sum = (house + space) % mod;
}
// as street has two side
return (int) ((sum * sum) % mod);
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).