2049. Count Nodes With the Highest Score

Problem

There is a binary tree rooted at 0 consisting of n nodes. The nodes are labeled from 0 to n - 1. You are given a 0-indexed integer array parents representing the tree, where parents[i] is the parent of node i. Since node 0 is the root, parents[0] == -1.

Each node has a score. To find the score of a node, consider if the node and the edges connected to it were removed. The tree would become one or more non-empty subtrees. The size of a subtree is the number of the nodes in it. The score of the node is the product of the sizes of all those subtrees.

Return **the *number* of nodes that have the highest score**.

  Example 1:

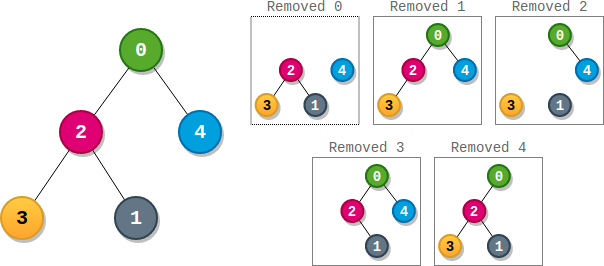
Input: parents = [-1,2,0,2,0]
Output: 3
Explanation:
- The score of node 0 is: 3 * 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 * 1 * 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.

Example 2:

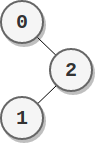
Input: parents = [-1,2,0]
Output: 2
Explanation:
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 * 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.

  Constraints:

• n == parents.length

• 2 <= n <= 10^5

• parents[0] == -1

• 0 <= parents[i] <= n - 1 for i != 0

• parents represents a valid binary tree.

Solution (Java)

class Solution {
    static class Node {
        Node left;
        Node right;
    }

    private int size;
    private long max;
    private int freq = 0;

    private long postOrder(Node root) {
        if (root == null) {
            return 0;
        }
        long left = postOrder(root.left);
        long right = postOrder(root.right);
        long val = Math.max(1, left) * Math.max(1, right) * Math.max(size - left - right - 1, 1);
        if (val > max) {
            max = val;
            freq = 1;
        } else if (val == max) {
            freq += 1;
        }
        return left + right + 1;
    }

    public int countHighestScoreNodes(int[] parents) {
        this.size = parents.length;
        Node[] nodes = new Node[size];
        for (int i = 0; i < size; i++) {
            nodes[i] = new Node();
        }
        Node root = null;
        for (int i = 0; i < size; i++) {
            if (parents[i] != -1) {
                Node node = nodes[parents[i]];
                if (node.left == null) {
                    node.left = nodes[i];
                } else {
                    node.right = nodes[i];
                }
            } else {
                root = nodes[i];
            }
        }
        postOrder(root);
        return freq;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).