Problem
Given the root of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
Example 1:
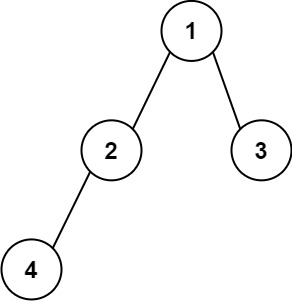
Input: root = [1,2,3,4]
Output: "1(2(4))(3)"
Explanation: Originally, it needs to be "1(2(4)())(3()())", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3)"
Example 2:
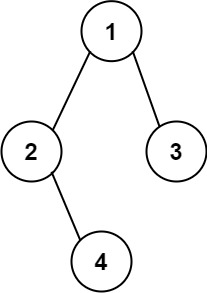
Input: root = [1,2,3,null,4]
Output: "1(2()(4))(3)"
Explanation: Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
Constraints:
The number of nodes in the tree is in the range
[1, 10^4].-1000 <= Node.val <= 1000
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public String tree2str(TreeNode t) {
if (t == null) {
return "";
}
StringBuilder sb = new StringBuilder();
preorder(t, sb);
return sb.toString();
}
private void preorder(TreeNode root, StringBuilder sb) {
if (root == null) {
return;
}
sb.append(root.val);
if (root.left != null) {
sb.append("(");
preorder(root.left, sb);
sb.append(")");
}
if (root.right != null) {
if (root.left == null) {
sb.append("()");
}
sb.append("(");
preorder(root.right, sb);
sb.append(")");
}
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).