Problem
A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.
Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
Example 1:
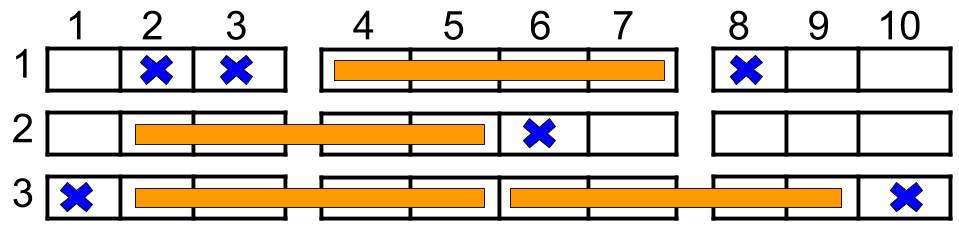
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
Example 2:
Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2
Example 3:
Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4
Constraints:
1 <= n <= 10^91 <= reservedSeats.length <= min(10*n, 10^4)reservedSeats[i].length == 21 <= reservedSeats[i][0] <= n1 <= reservedSeats[i][1] <= 10All
reservedSeats[i]are distinct.
Solution (Java)
class Solution {
public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
Map<Integer, int[]> occupiedFamilySeats = new HashMap<>();
for (int[] reservedSeat : reservedSeats) {
int row = reservedSeat[0];
int col = reservedSeat[1];
if (col == 1 || col == 10) {
continue;
}
int[] rowFamilySeats = occupiedFamilySeats.getOrDefault(row, new int[3]);
if (col == 2 || col == 3) {
// mark left family seating as occupied
rowFamilySeats[0] = 1;
occupiedFamilySeats.put(row, rowFamilySeats);
}
if (col == 8 || col == 9) {
// mark right family seating as occupied
rowFamilySeats[2] = 1;
occupiedFamilySeats.put(row, rowFamilySeats);
}
if (col == 4 || col == 5) {
// mark left family seating as occupied
rowFamilySeats[0] = 1;
// mark min family seating as occupied
rowFamilySeats[1] = 1;
occupiedFamilySeats.put(row, rowFamilySeats);
}
if (col == 6 || col == 7) {
// mark min family seating as occupied
rowFamilySeats[1] = 1;
// mark right family seating as occupied
rowFamilySeats[2] = 1;
occupiedFamilySeats.put(row, rowFamilySeats);
}
}
// max number of family seats per row is 2, so we start that minus the rows for which we
// have reservations
int count = n * 2 - 2 * occupiedFamilySeats.size();
// for each row with reservations, count remaining family seatings
for (int[] familySeats : occupiedFamilySeats.values()) {
if (familySeats[0] == 0) {
count++;
}
if (familySeats[2] == 0) {
count++;
}
if (familySeats[0] != 0 && familySeats[2] != 0 && familySeats[1] == 0) {
count++;
}
}
return count;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).